Home
Browsing Animations: Forces
40 Animations
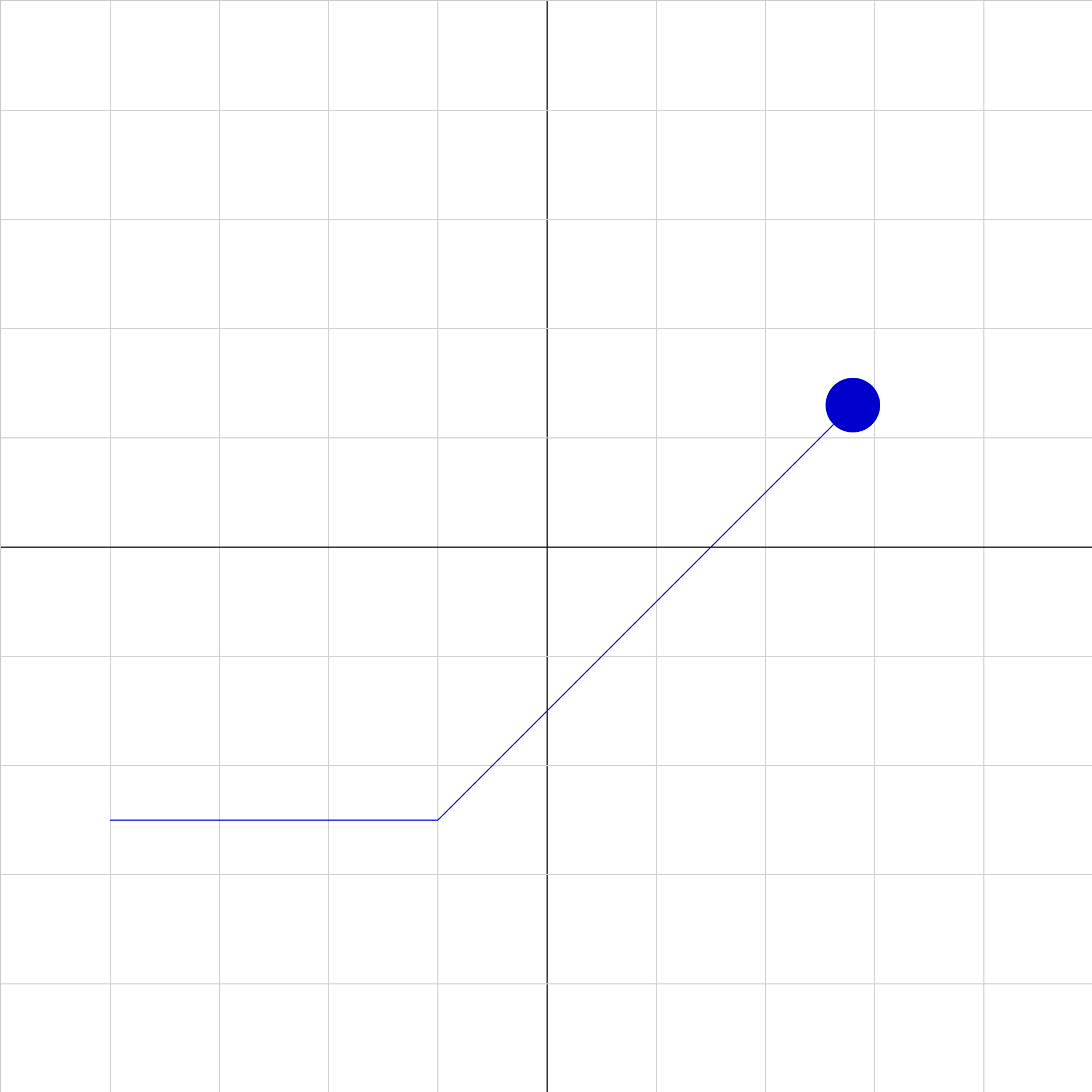
2dforce-01a.iwp
The view is looking down on an air hockey table. A puck initially moving at constant velocity receives a momentary push in the +y direction at x = -2 as shown in each of the animations (selectable by numbers 1 to 4). Which animation correctly shows the motion of the puck after it is pushed?
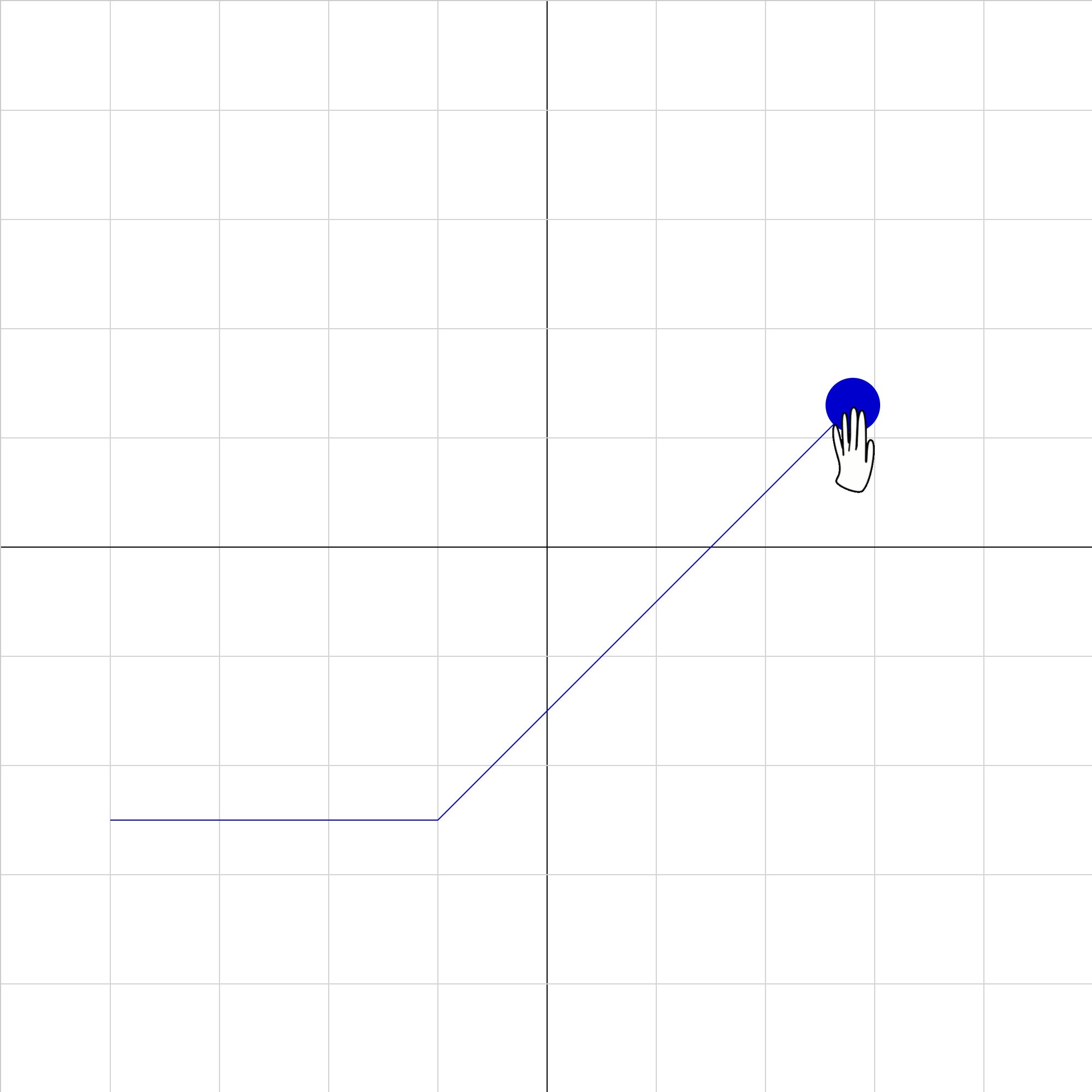
2dforce-01b.iwp
A satellite moves at constant velocity when, at x = -2, its thrusters are suddenly engaged, producing a constant force perpendicular to its original motion. Which animation correctly depicts the satellite's motion after the thrusters are first engaged?

Gravity-Animation-Template.iwp
A blue object orbits a large, fixed mass at the origin. The power of the gravitational force on each of the orbiting objects can be adjusted according to a number of parameters: the mass of each object; the gravitational constant G. In reality, the gravitational force is exactly inversely proportional to the square of the distance between the orbiting object and the origin. This animation replicates this force, but we might also be interested in the behavior of gravity at different powers. Using the designer, edit this animation to allow the user to input a gravitational power which changes the behavior of gravity. In order to compare this generalized gravitational scheme to reality, include two oribiting objects, each with inputtable parameters.
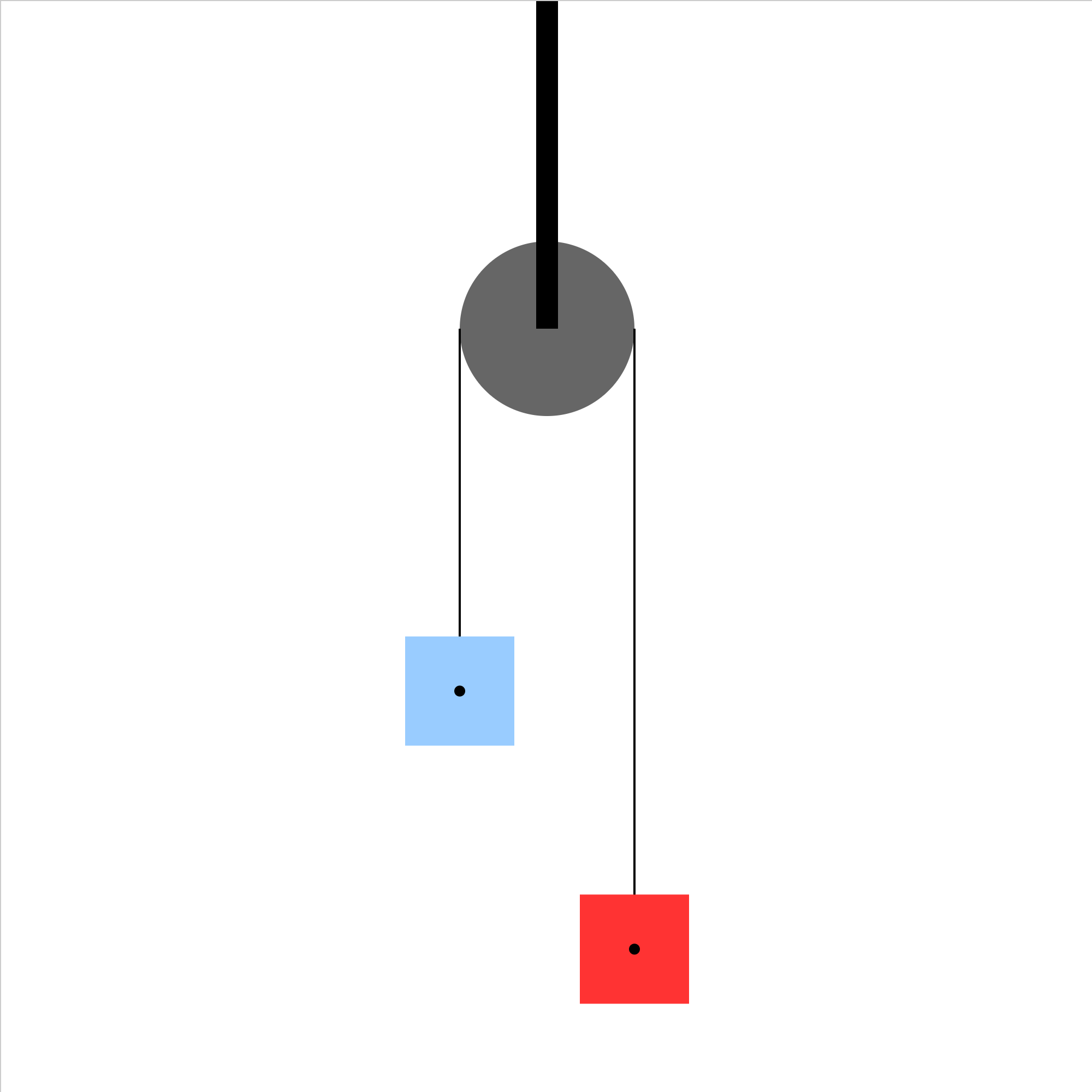
atwoods-01.iwp
Two blocks are connected by a massless, unstretchable string which passes over a frictionless, massless pulley. The pulley is supported from above. When the blocks are released, the system of the two blocks accelerates. What is the acceleration of the system? Caution: Unphysical results will be obtained if blocks slide past the pulley.
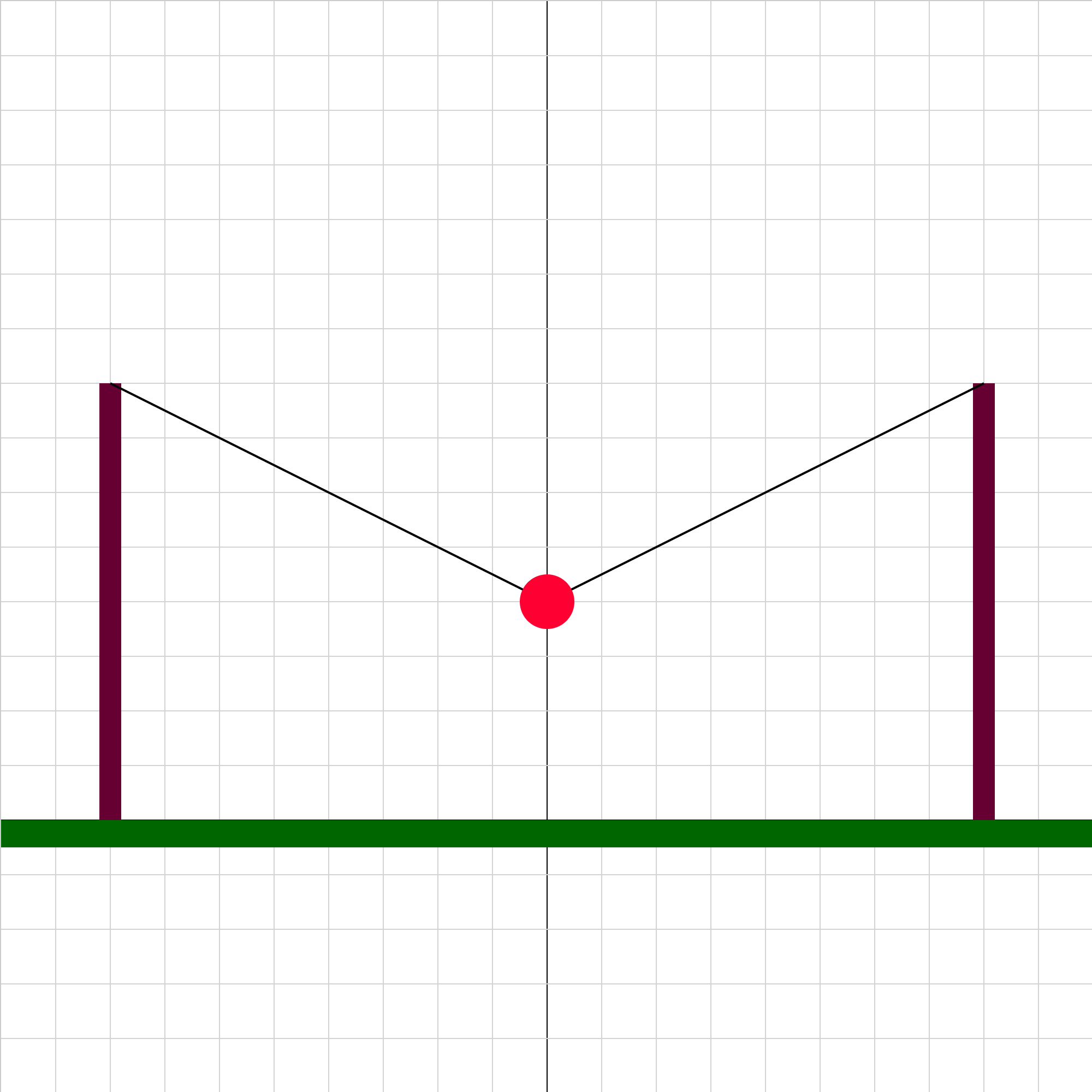
equilibrium-01.iwp
A ball is suspended by strong wires from two posts. What are the magnitudes and directions of the forces on the ball?
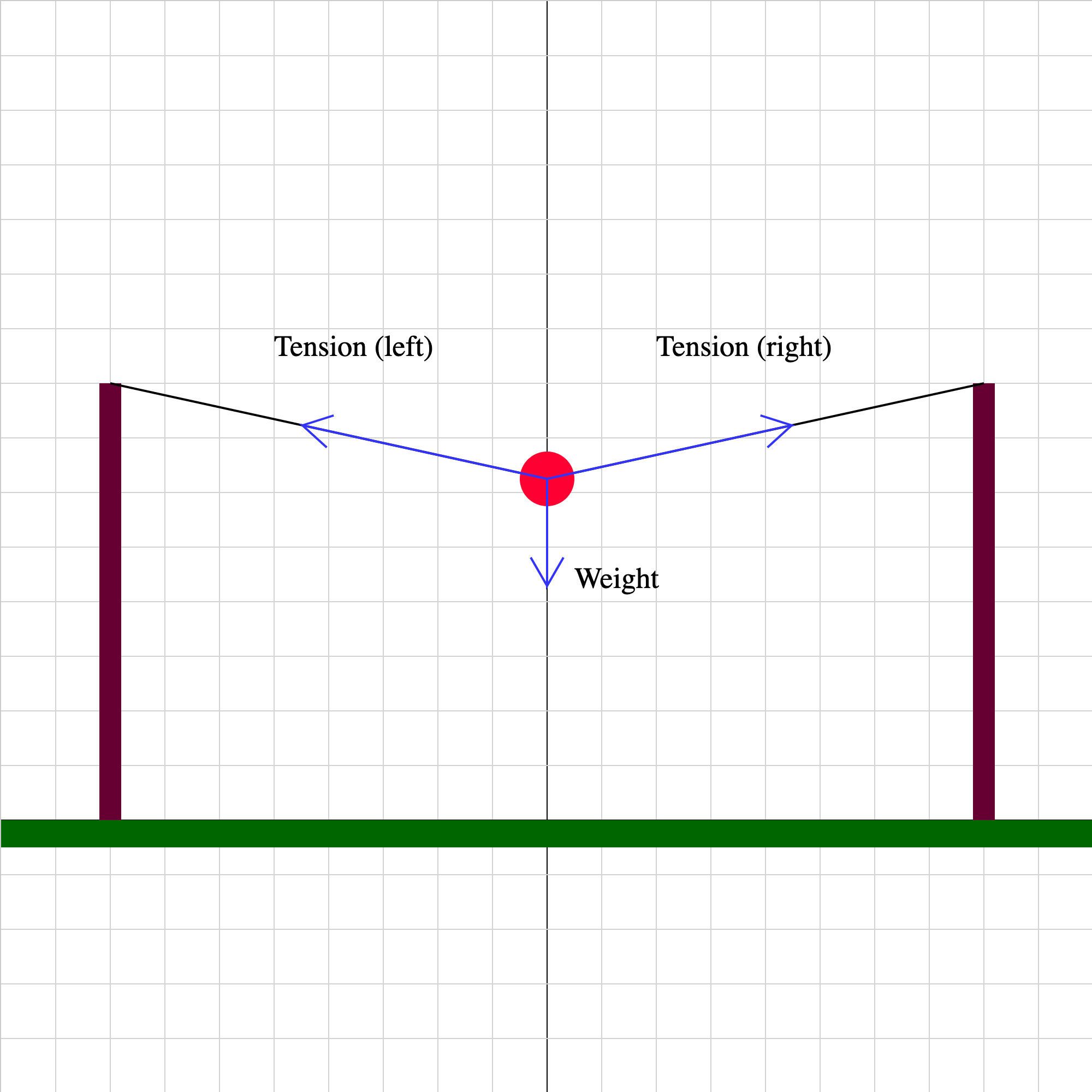
equilibrium-02.iwp
A ball is suspended by strong wires from two posts. The tension forces and weight are shown. Step through the animation using the >> button to see how the forces change for different vertical positions of the ball.
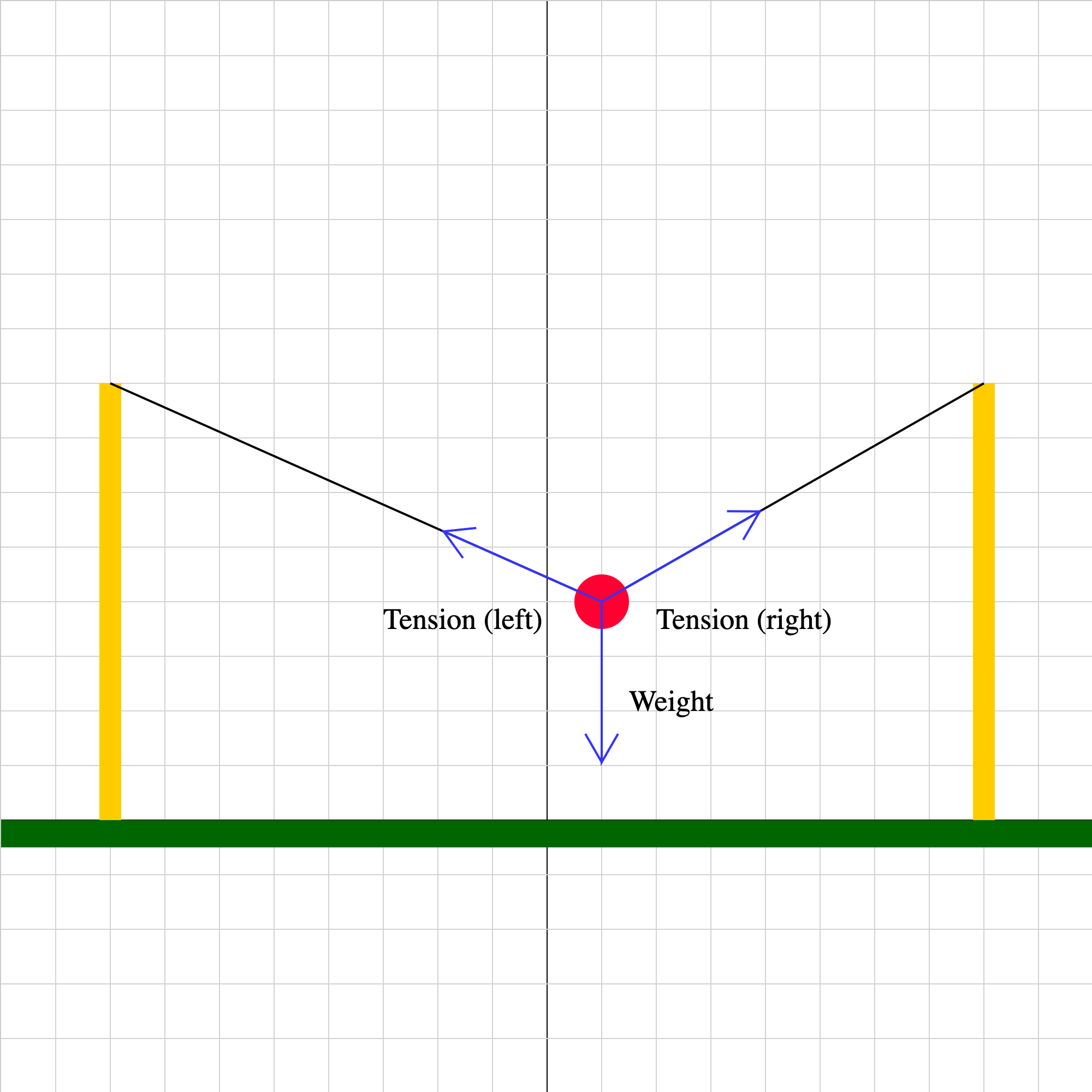
equilibrium-03b.iwp
A ball is suspended by strong wires from two posts. The tension forces and weight are shown. Step through the animation using the >> button to see how the forces change for different horizontal positions of the ball.
fallcompare-simulation.iwp
The green ball falls in a vacuum, while the red ball experiences a drag force from the fluid in which it falls. The acceleration of the red ball is a = -g + kv**2, where g = 9.8 N/kg, v is the speed of the ball, and k is a coefficient (which we term the drag factor) that depends on characteristics of the ball and the fluid. You may change the value of k to see how that influences the red ball. The vertical separation of the two balls is displayed in the list of outputs.

friction01b.iwp
A red box slides down a wall. The box is in motion at t = 0. A constant force (for example, from a hand) is applied on the box to the right. The grid spacing is 1 meter. Assume the axis directions shown.

friction01c.iwp
A red box slides down a wall. The forces on the box are shown. Try changing the parameters (mass of box, coefficient fo kinetic friction, applied force) to see how that affects the force vectors.
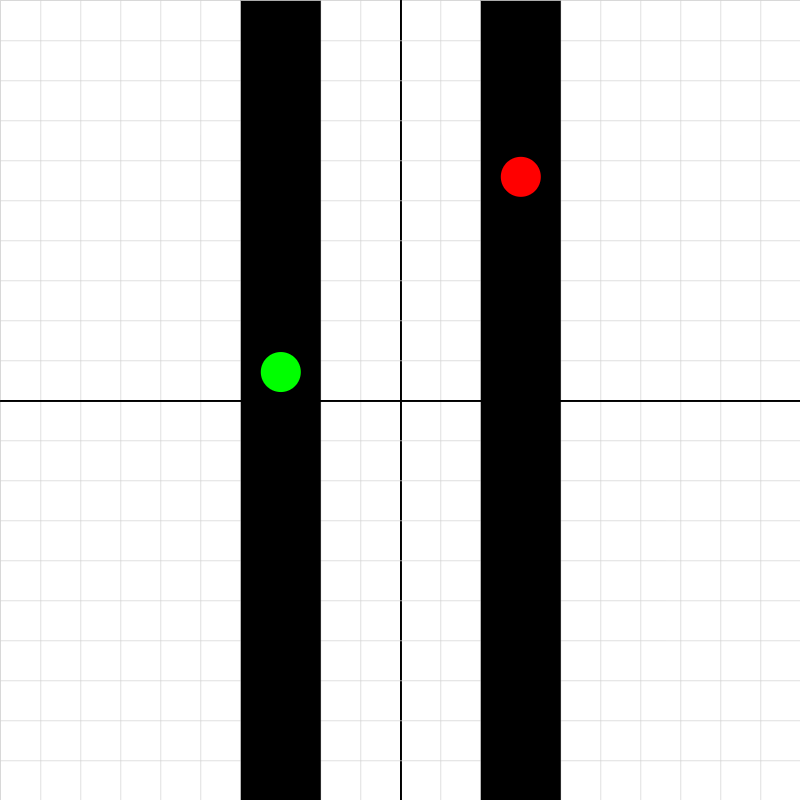
gravitation-01b.iwp
A satellite orbits the Earth in a circular orbit. The ratio of the radius of the satellite's orbit to the radius of the Earth is given. The red dot represents an apple falling near the surface of the Earth. The distance fallen is too small in scale compared to planetary distances to see in the animation. However, the acceleration is greater than that of the satellite. The vectors represent the accelerations of the objects.
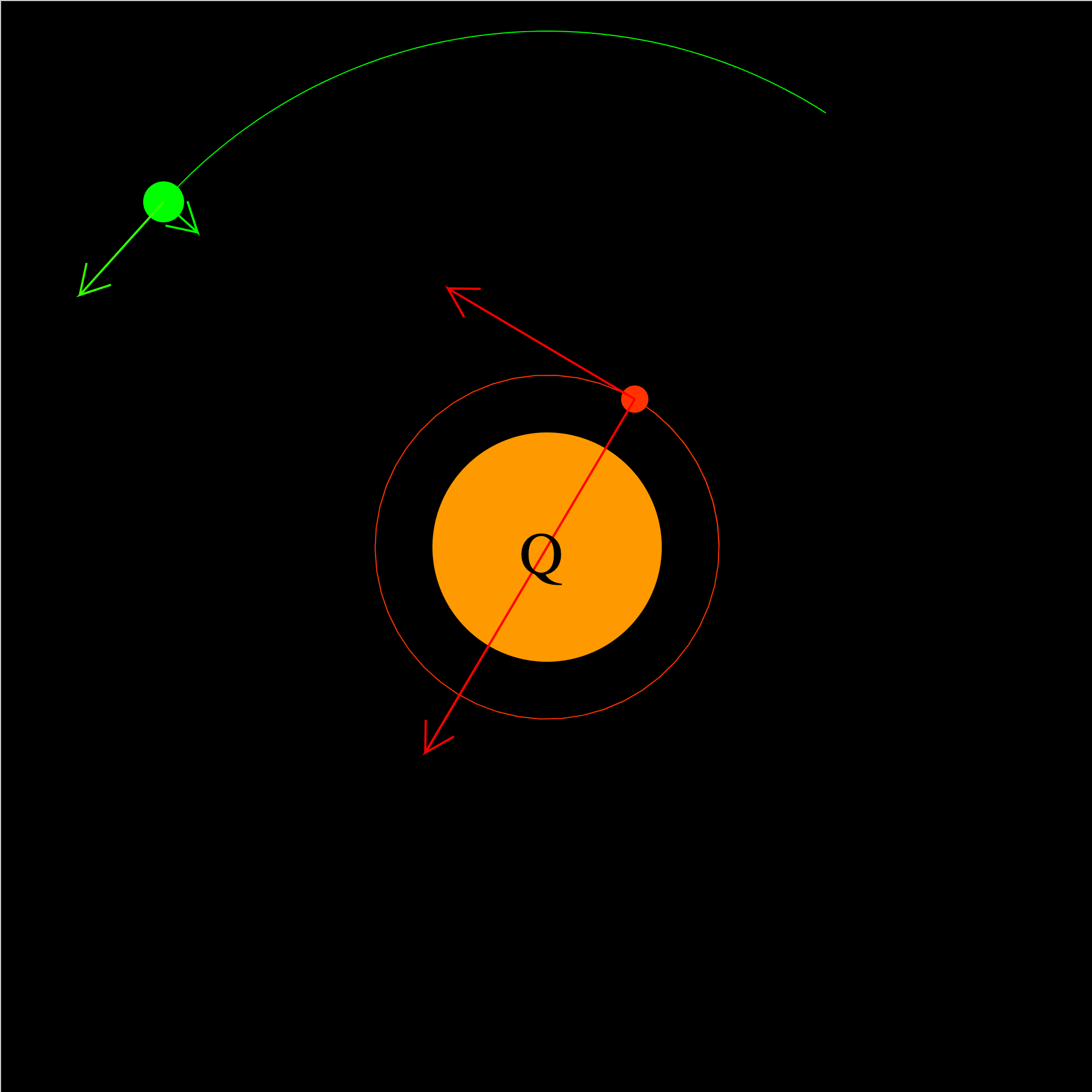
gravitation-01e.iwp
Two satellites orbit Planet Q in circular orbits. The ratios of the orbital radii and of the masses of the satellites are given. The vectors represent the gravitational accelerations and orbital velocities of the satellites.

gravitation-02b.iwp
The space shuttle orbits the Earth. The ratio of the shuttle's orbital radius to the Earth is given. The view is looking down on a pole. The white line represents a meridian. Hence, it rotates at the same frequency as the Earth.
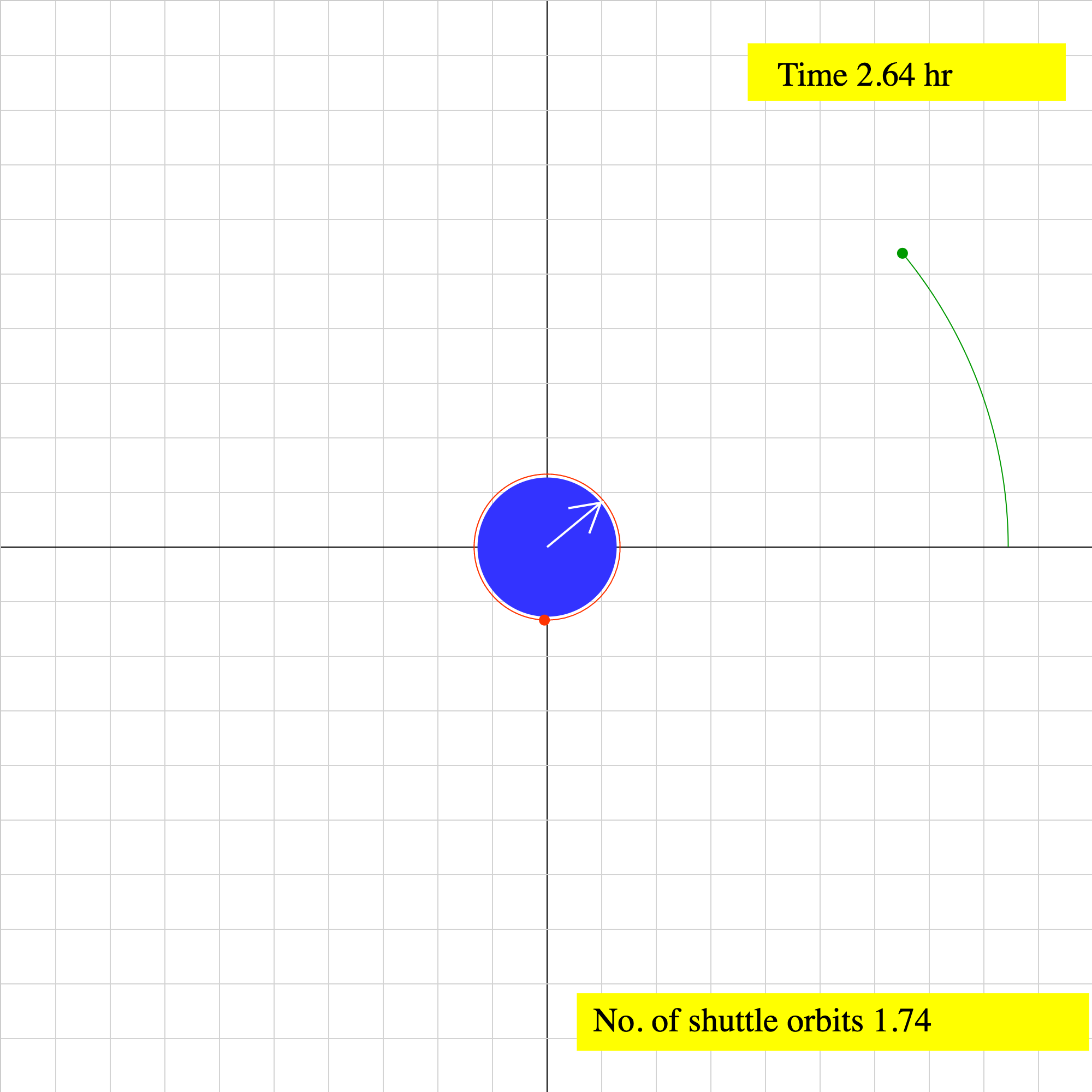
gravitation-03.iwp
The green satellite orbits the Earth in a geostationary orbit. This means that the satellite orbits in the Earth's equatorial plane and always remains above the same point on the Earth. The rotation of the Earth is repesented by the white arrow, which points directly to the satellite. The elapsed time is given in both hours and seconds. The red satellite orbits the Earth in a typical space shuttle orbit. This orbit is very close to the Earth in comparison to that of the geosynchronous satellite. A readout of the number of shuttle orbits executed is given.
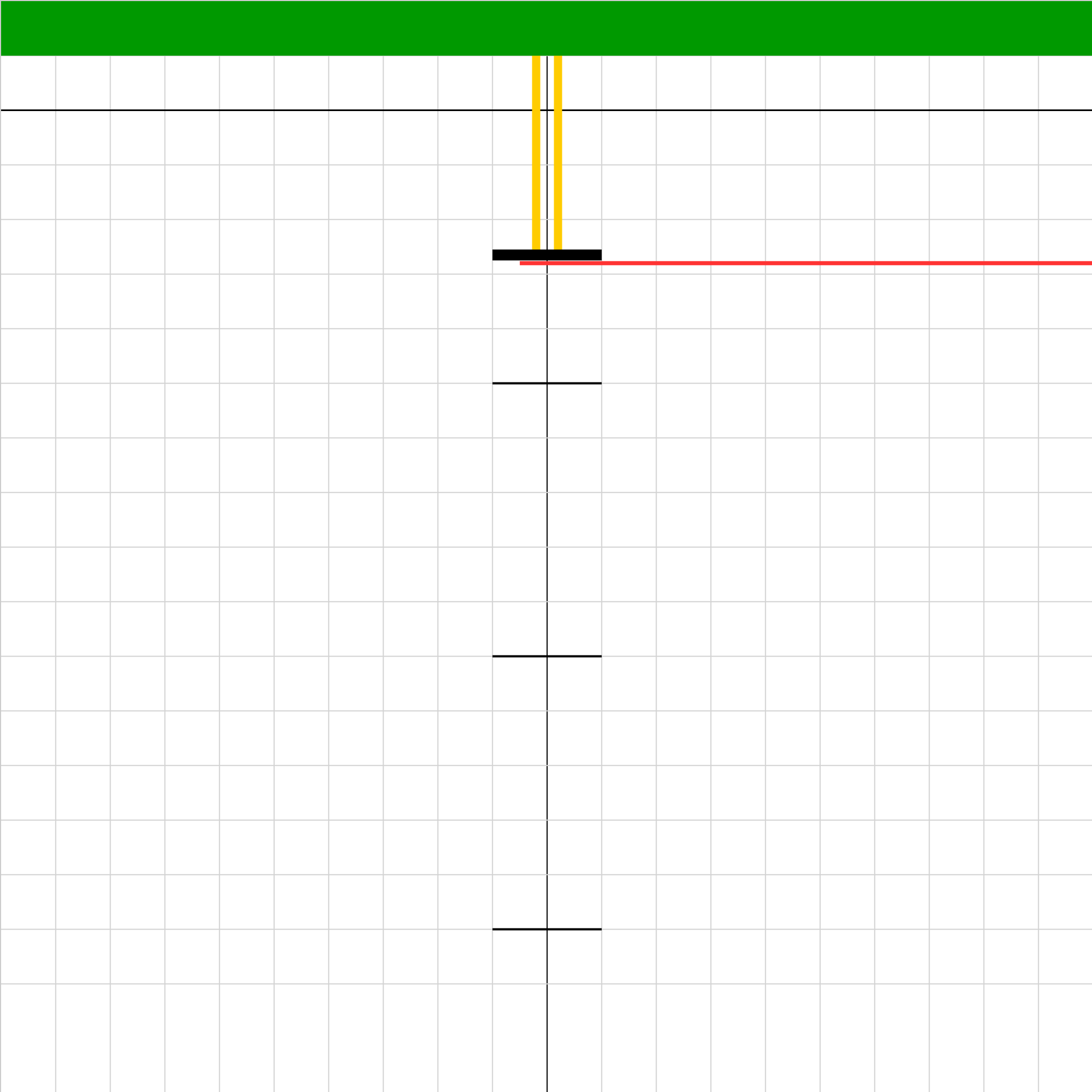
hookeslaw03.iwp
A platform (black) is suspended from a fixed support by a rubber band. Weight can be added to the platform. When the red stick is pulled away, the platform with its weight will oscillate vertically and eventually come to rest at its equilibrium position. The goal of the problem is to take data to find the spring constant of the rubber band and to find the mass of the platform. For the latter, you'll need one measurement other than those described below. With platform held in place by the stick, the rubber band is unstretched. Click the play buttom to pull the stick away quickly and let the platform fall. After the platform reaches its resting position, read the position to the nearest 0.001 m. (In order to make the motion damp more quickly, increase the value of the damping coefficient.) Add 0.1 kg of mass to the plaform and click Reset. Then play the animation to see the new equilibrium position. Record the reading. Continue to add mass in increments of 0.1 kg and measure the equilibrium position each time. Tic marks are placed every 0.05 m to aid in taking readings.
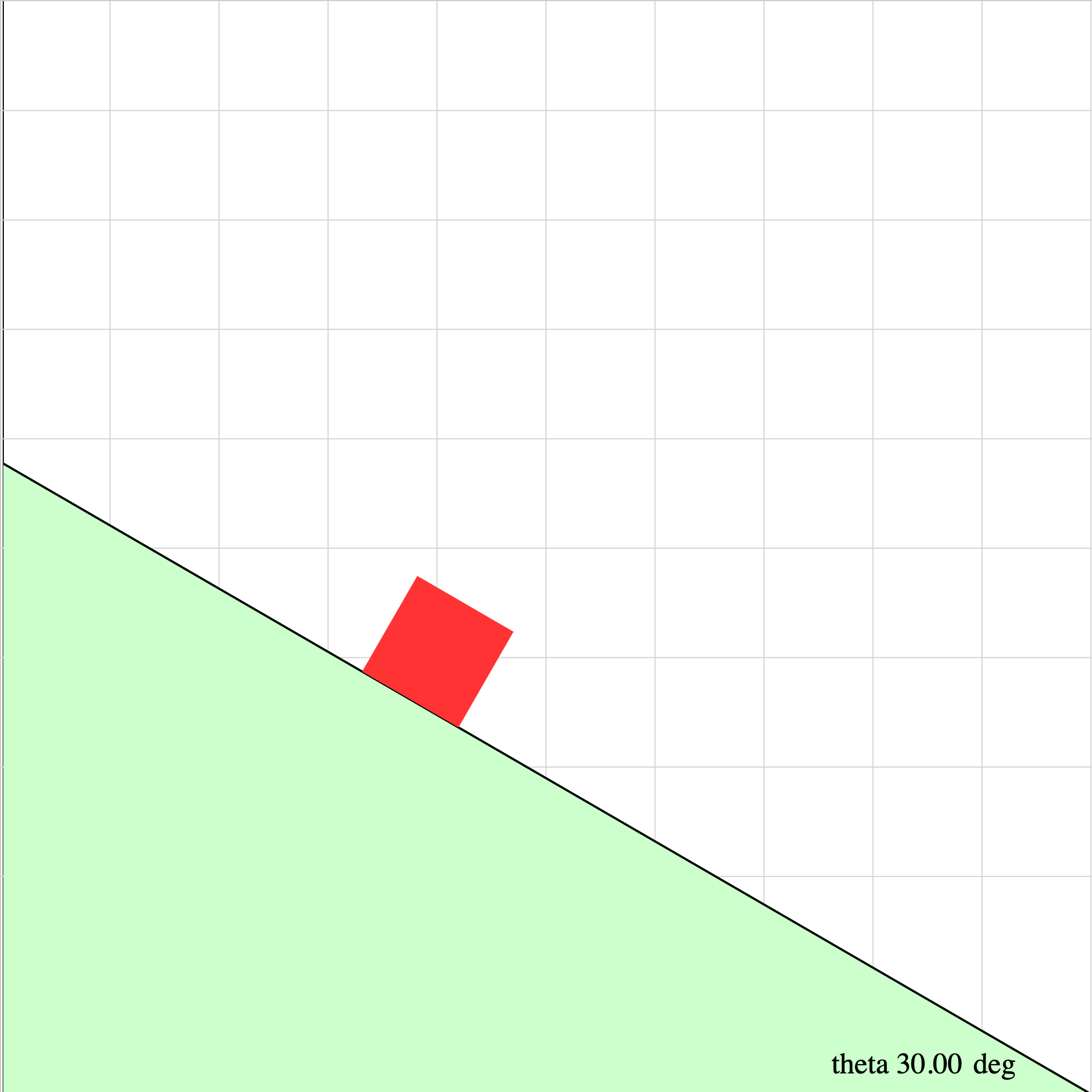
incplane04.iwp
An object slides down a frictionless inclined plane. The plane makes an angle of theta with the horizontal.
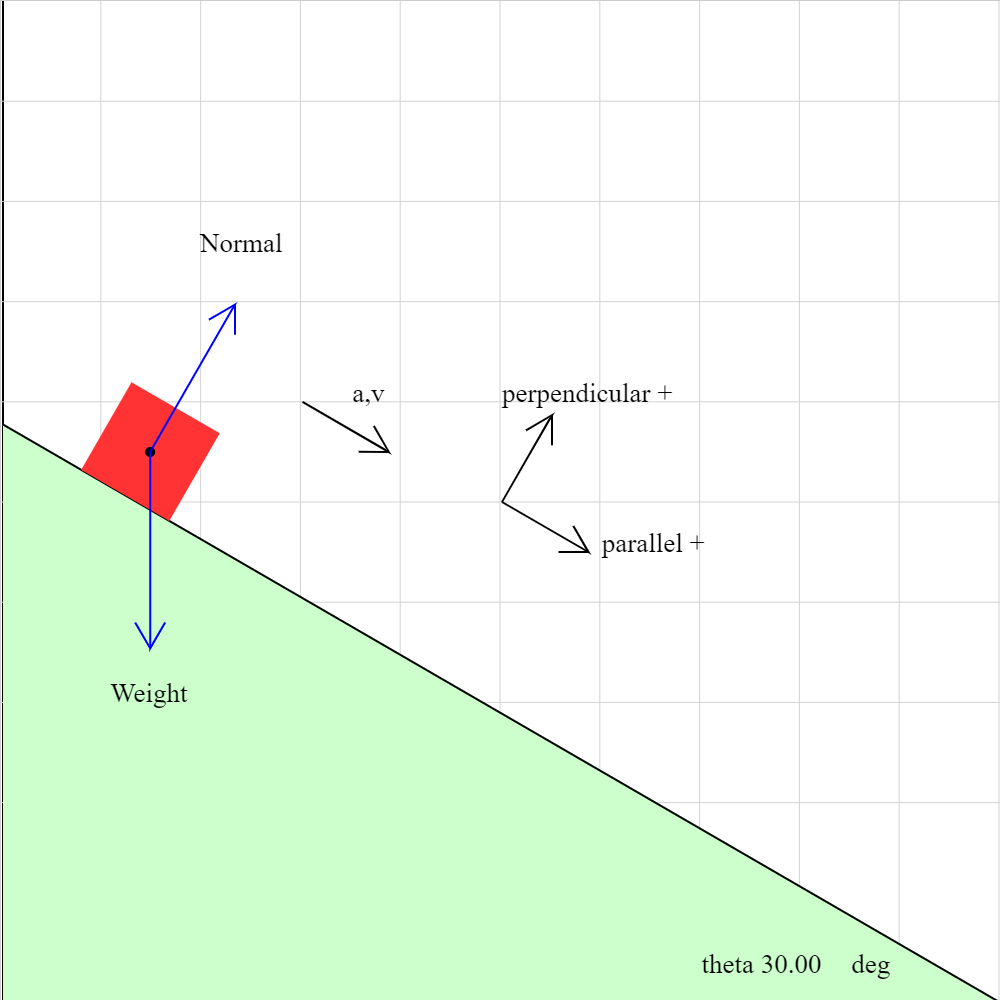
incplane04b.iwp
An object slides down a frictionless plane. The plane makes an angle theta with the horizontal. The forces acting on the object are the normal force acting perpendicular to the plane and the weight acting vertically downward.
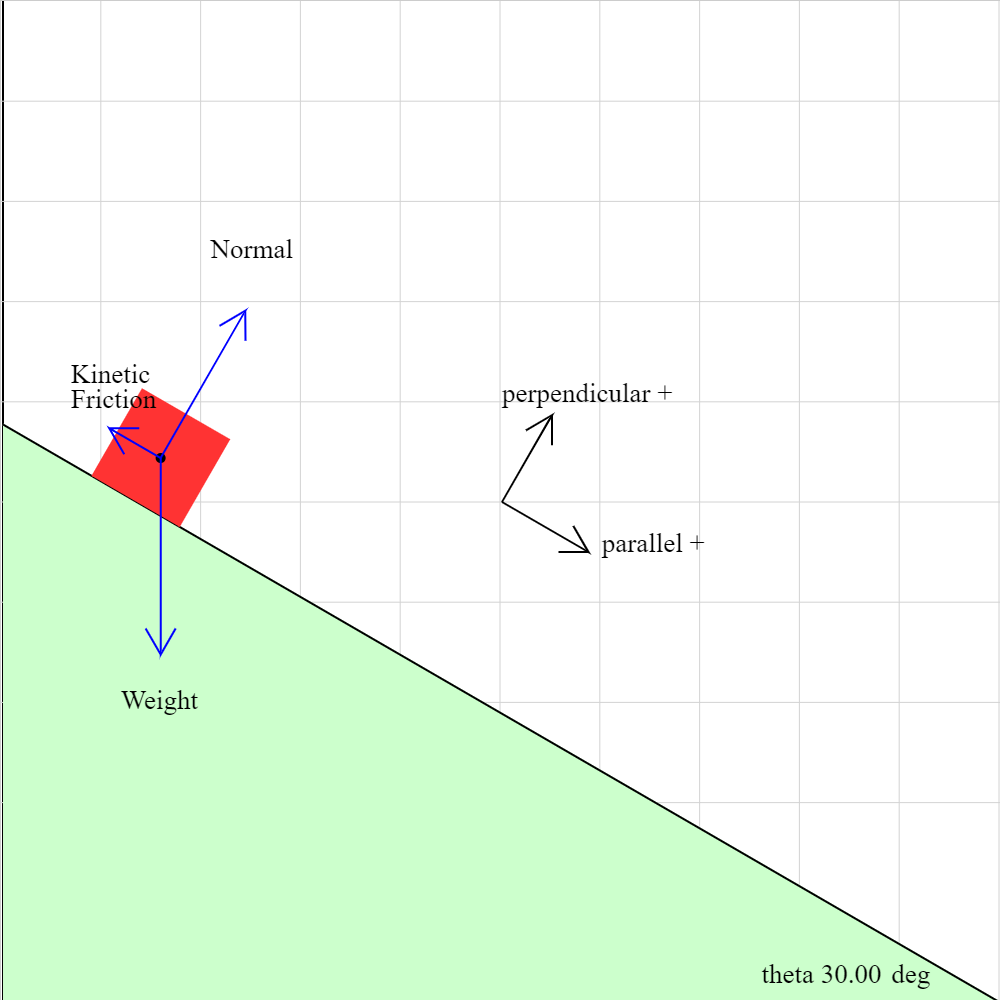
incplane04c.iwp
An object slides down a plane. In addition to the weight and normal force, kinetic friction acts on the object.

incplane05.iwp
An object slides down an inclined plane. The coefficient of kinetic friction, which is initially 0, can be changed. The inclination of the plane, the initial x-coordinate of the block, and the initial velocity can also be changed. Vectors in black represent the fores acting on the plane. The vector in red is the net force. The scale factor may be changed to increase or decrease the size of all the vectors by the same factor.
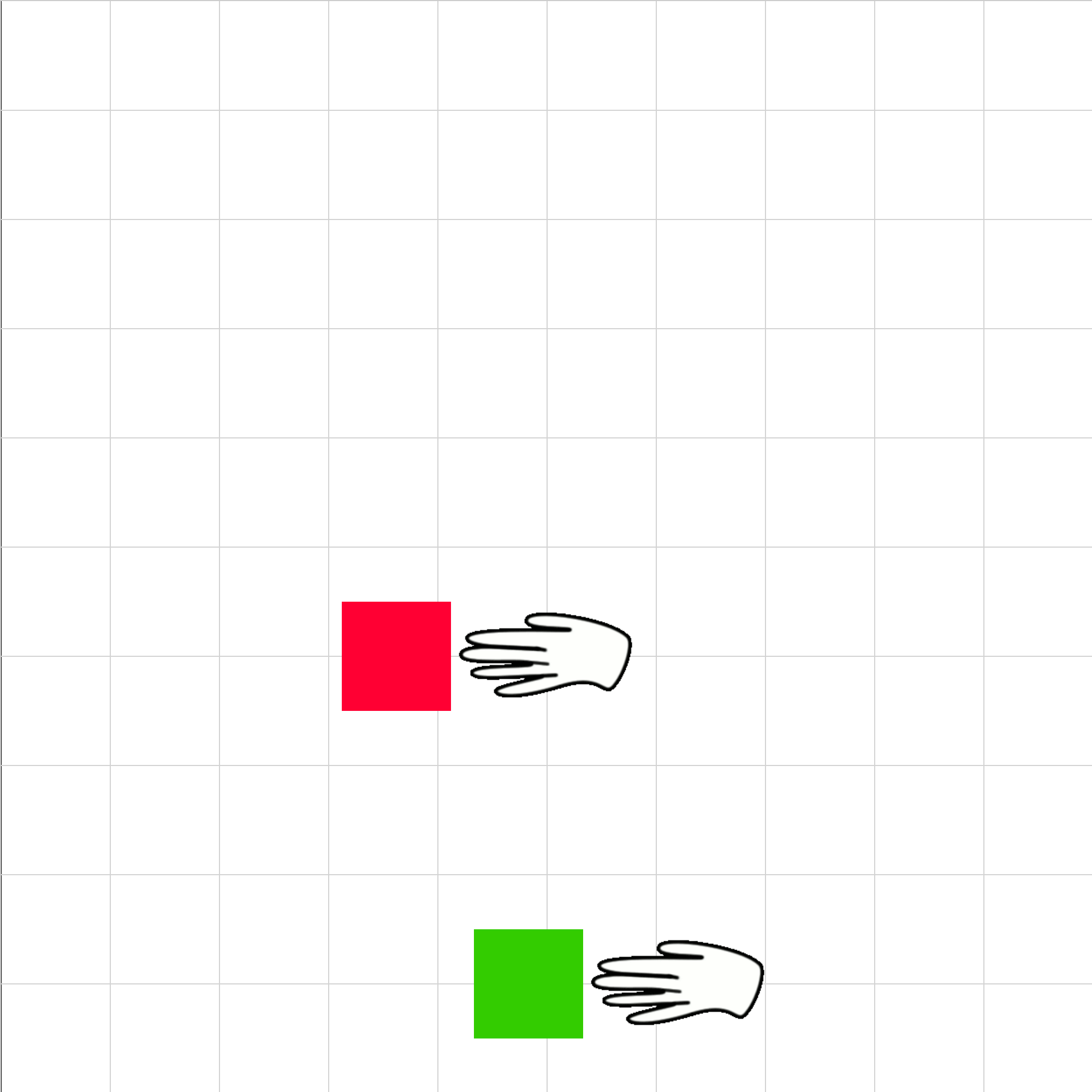
nsl-00.iwp
Two blocks initially rest next to each other on a frictionless surface. (The view is looking down on the surface.) At t = 0, an identical push is applied directly to each block. The push on each block remains constant as the blocks accelerate. Which block has more mass and why.

nsl-01.iwp
Two blocks rest next to each other on a frictionless surface. At t = 0, a push (by a hand for example) is applied directly to the green block. The push remains constant as the two blocks accelerate.
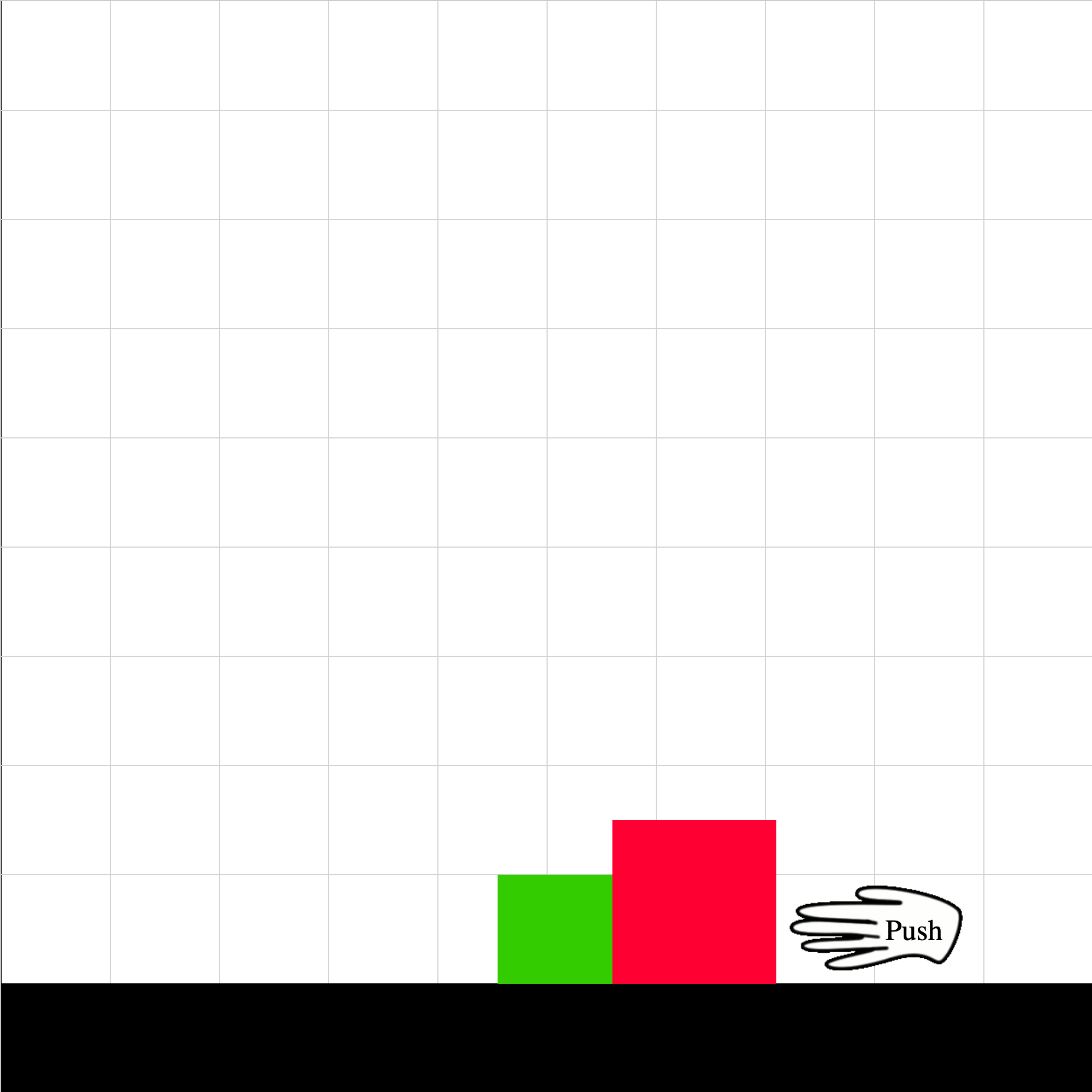
nsl-02.iwp
Two blocks rest next to each other on a frictionless surface. At t = 0, a push (by a hand for example) is applied directly to the red block. The push remains constant as the two blocks accelerate.

pendulum02.iwp
A pendulum is released from rest and oscillates in a vertical plane. For which positions (A, B, C) is the tangential acceleration 0? maximum? centripetal acceleration 0? maximum?

pendulum03.iwp
A pendulum is set up on the surface of Planet X. The bob is released from rest and oscillates in a vertical plane. What is the acceleration due to gravity on the surface of Planet X?
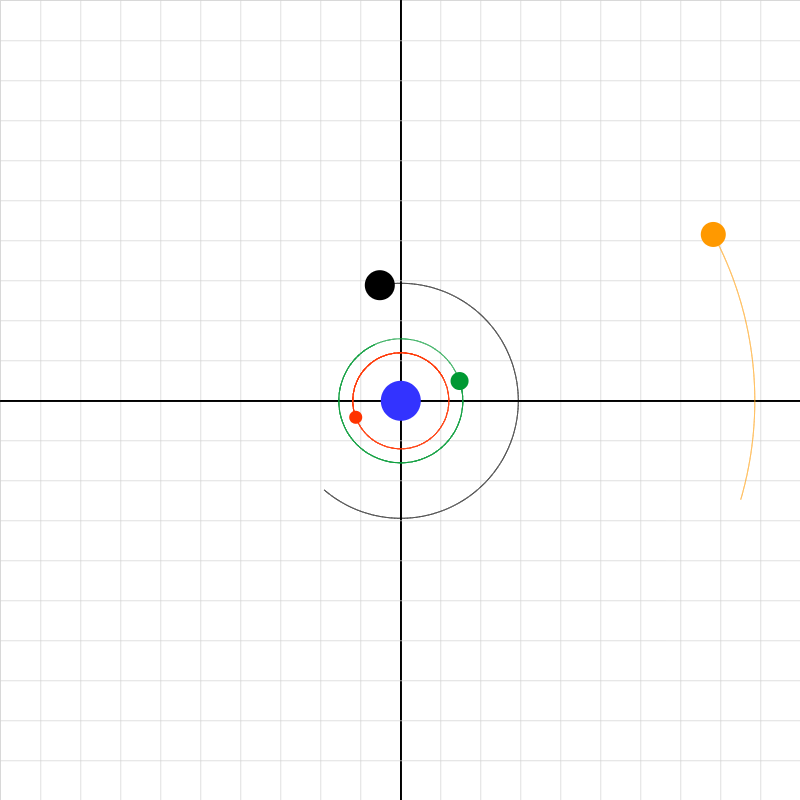
planetary-system-02.iwp
Four moons revolve around a planet in circular orbits. Determine the period and radius of each orbit. Use the buttons on the right to start/stop the animation and step it frame-by-frame. Readouts of time and position coordinates are displayed above the buttons.
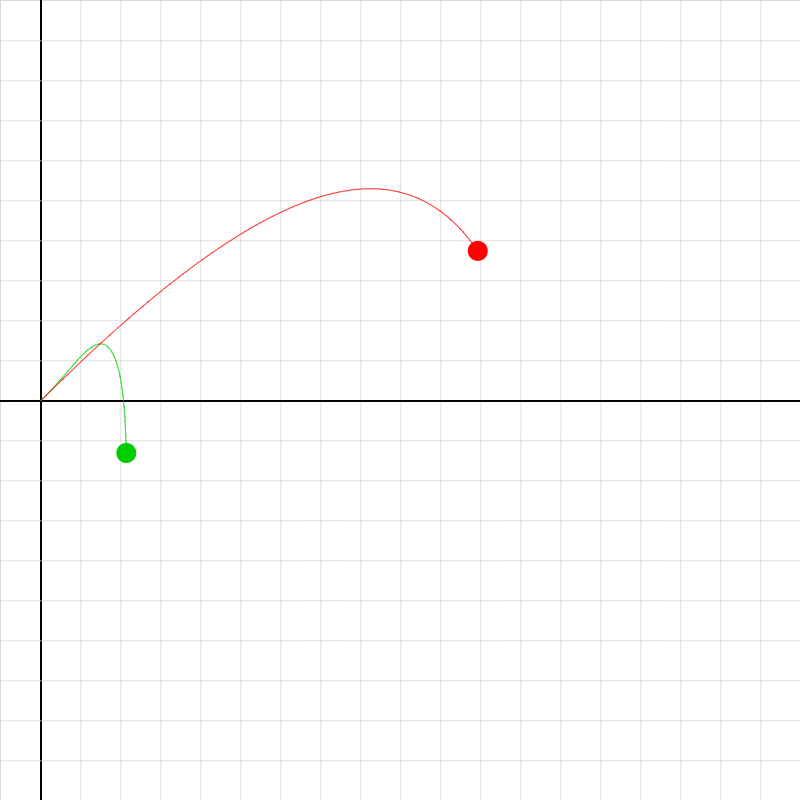
projectile-drag-2.iwp
The green projectile is subject to a v-squared drag force. The red projectile is subject to a v drag force.

projectile-drag-lift-2.iwp
The projectile is subject to a downward gravitational field, a drag force opposing the velocity and proportional to v-squared, and a lift force proportional to and perpendicular to the velocity.
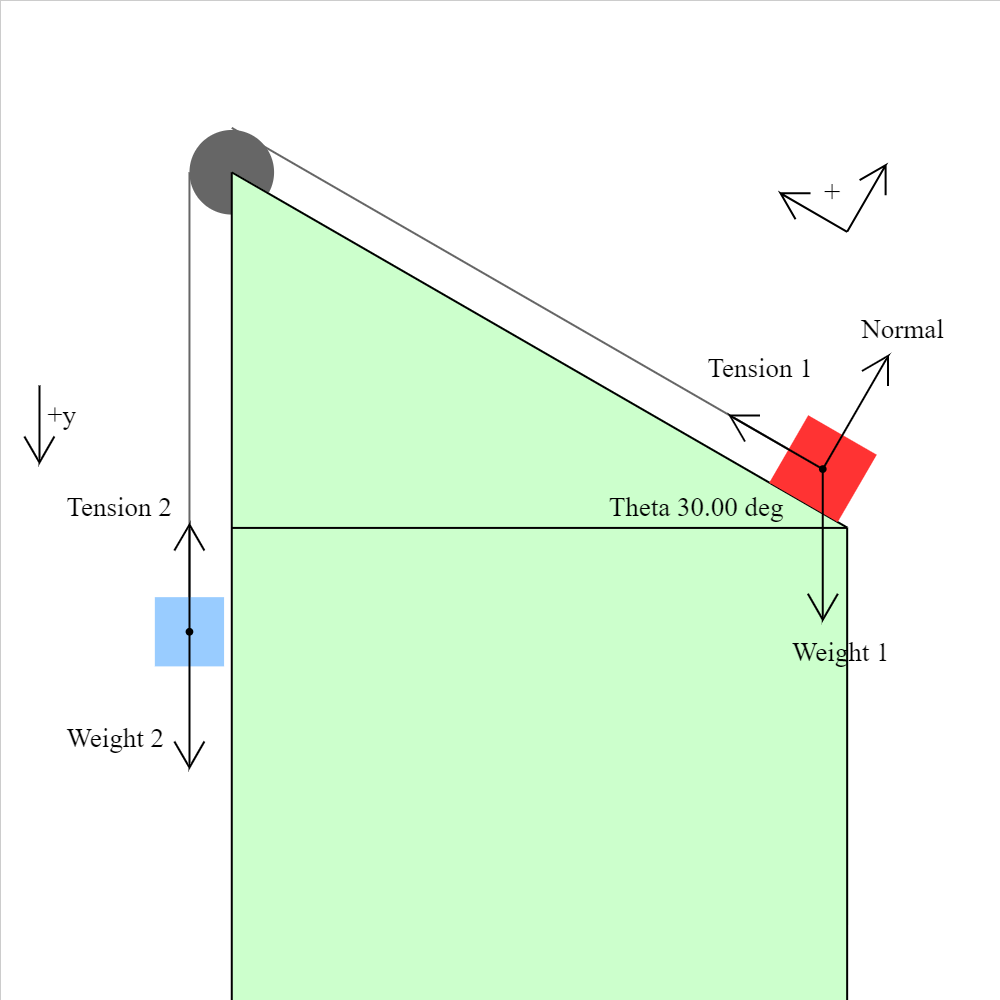
pulley-plane-03.iwp
Two blocks are connected by a massless, unstretchable string which passes over a frictionless, massless pulley. There is no friction between the red block and the plane. When the blue block is released, the system of the two blocks accelerates. The forces on the blocks are shown. Caution: Unphysical results may be obtained with certain combinations of masses and angle.
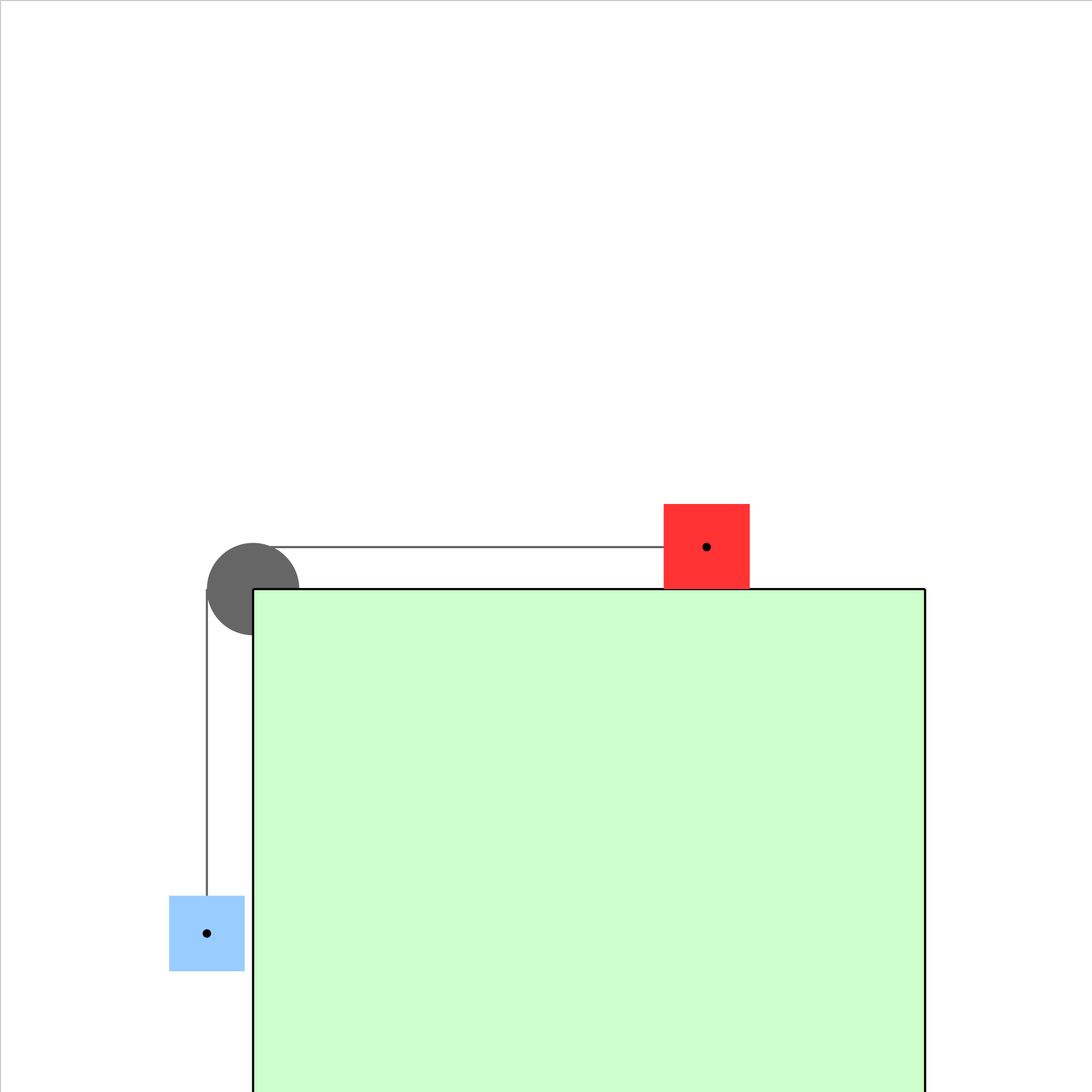
pulley-plane-04.iwp
Two blocks are connected by a massless, unstretchable string which passes over a frictionless, massless pulley. There is no friction between the red block and the plane. When the blue block is released, the system of the two blocks accelerates. What is the acceleration of the system? Caution: Unphysical results will be obtained if blocks slide past the table boundaries.
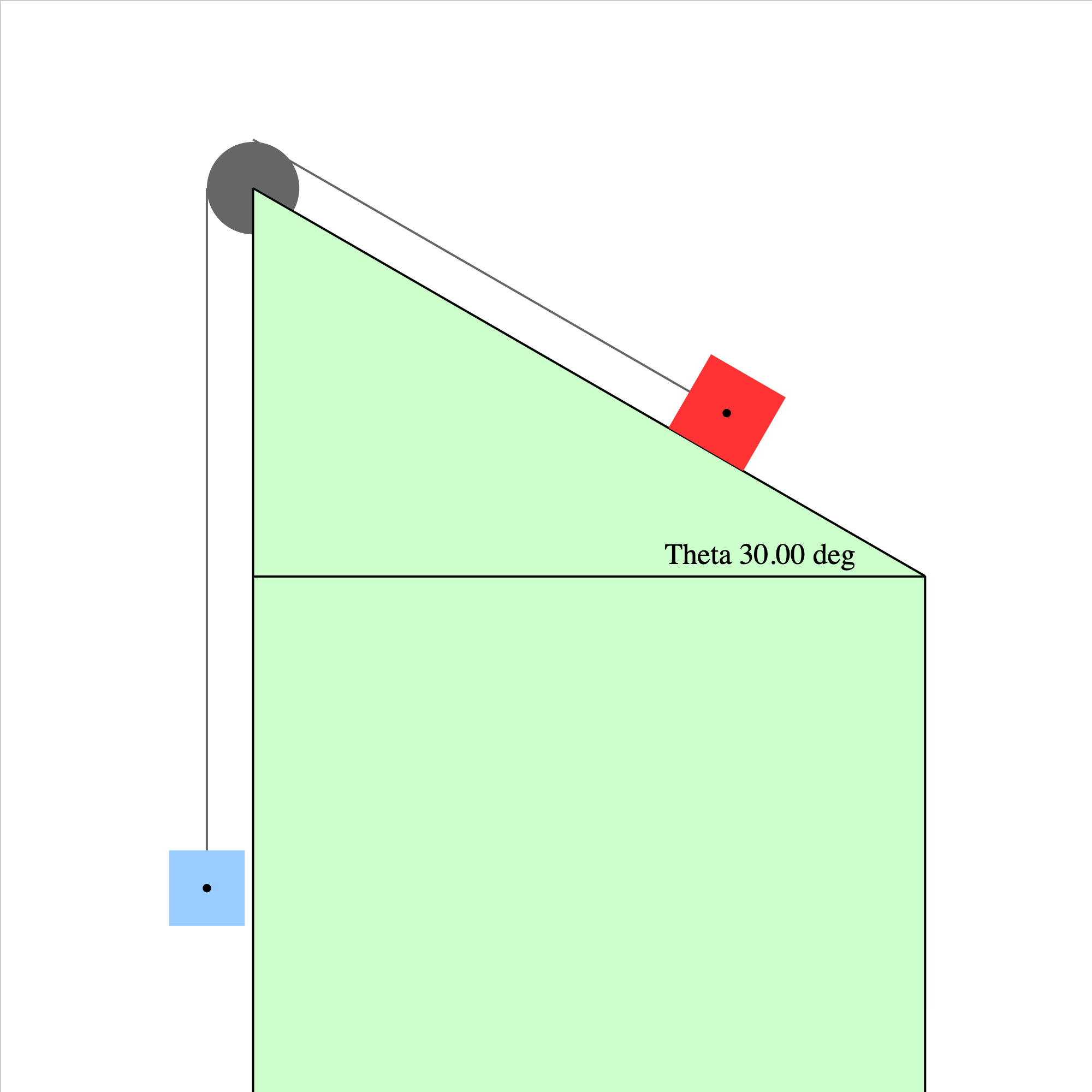
pulley-plane-05.iwp
Two blocks are connected by a massless, unstretchable string which passes over a frictionless, massless pulley. There is no friction between the red block and the plane. When the blue block is released, the system of the two blocks accelerates. What is the acceleration of the system? How must the masses compare in order for the system of the two blocks to be in equilibrium? Caution: Unphysical results may be obtained with certain combinations of masses.
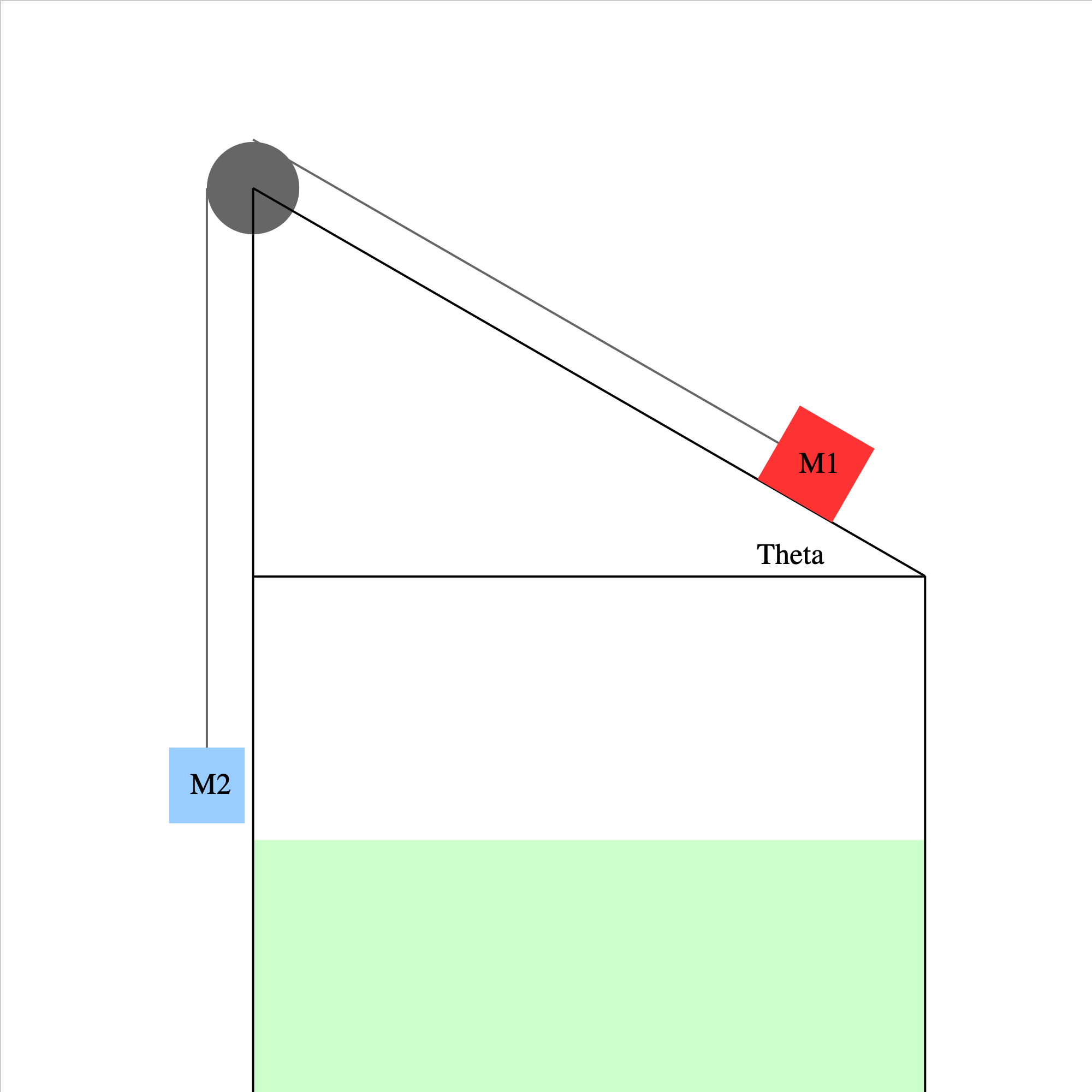
pulley-plane-05a.iwp
Two blocks are connected by a massless, unstretchable string which passes over a frictionless, massless pulley. There is no friction between the red block and the plane. When the blue block is released, the system of the two blocks accelerates. What is the acceleration of the system and the tension in the connecting string in terms of the masses, the angle of inclination, and g?
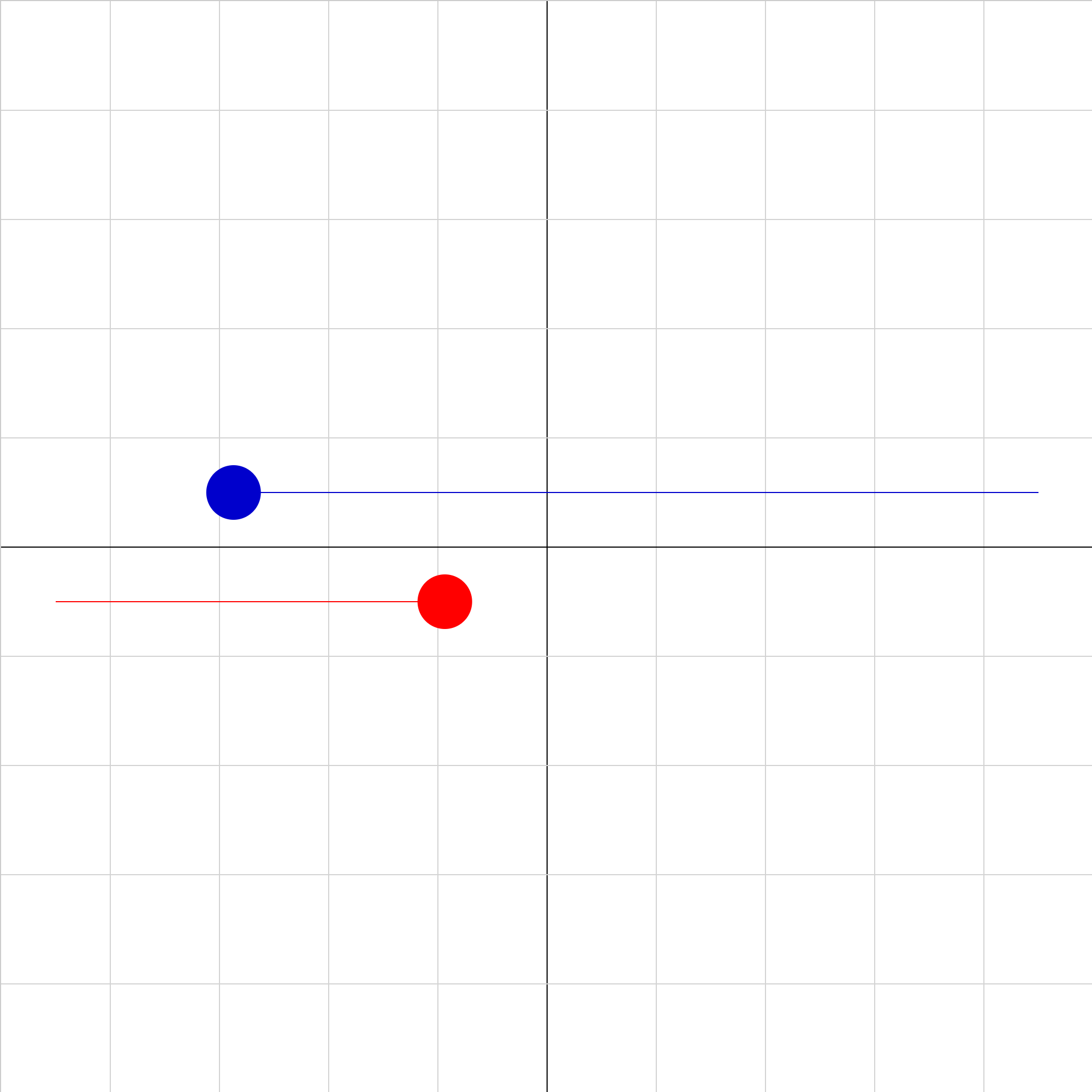
shm-phase-02b.iwp
The red and blue objects have the same mass and oscillate in SHM with the same period and amplitude. The only thing different is the phase. Click Show Graph to see position vs. time graphs of both objects. Determine what the phase of the blue object must be so that it starts at the same position and with the same velocity and acceleration as the red object. You can check your answer by inputing the value of phase that you calculate. Note that the phase is input in radians.
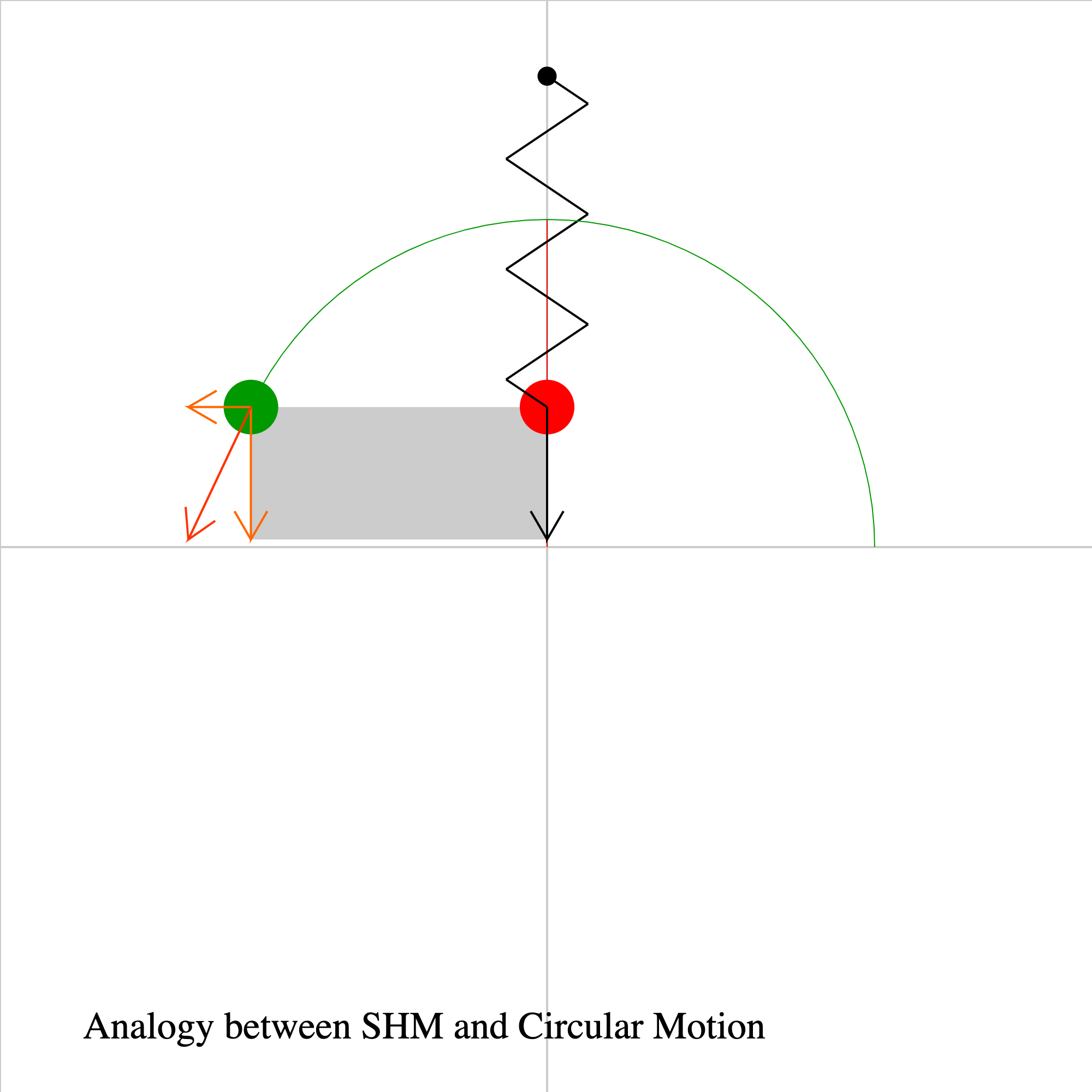
spring-circle-analogy-02.iwp
A ball oscillates in simple harmonic motion about the origin, while a second ball moves at constant speed in a circular path. Both balls start at y = 0 and have the same initial velocity. The black vector represents the velocity of the red ball, and the orange vectors represent the total velocity and the x- and y-velocity components of the green ball. The speed of the green ball and the angle that its radius vector makes with the +x-axis are given under Outputs. At all times, the position and velocity of the red ball are equal to the y-components of the position and velocity of the green ball. It may be helpful to think of the motion of the red ball as the projection of the motion of the green ball onto the y-axis. This is what the gray shadow represents.
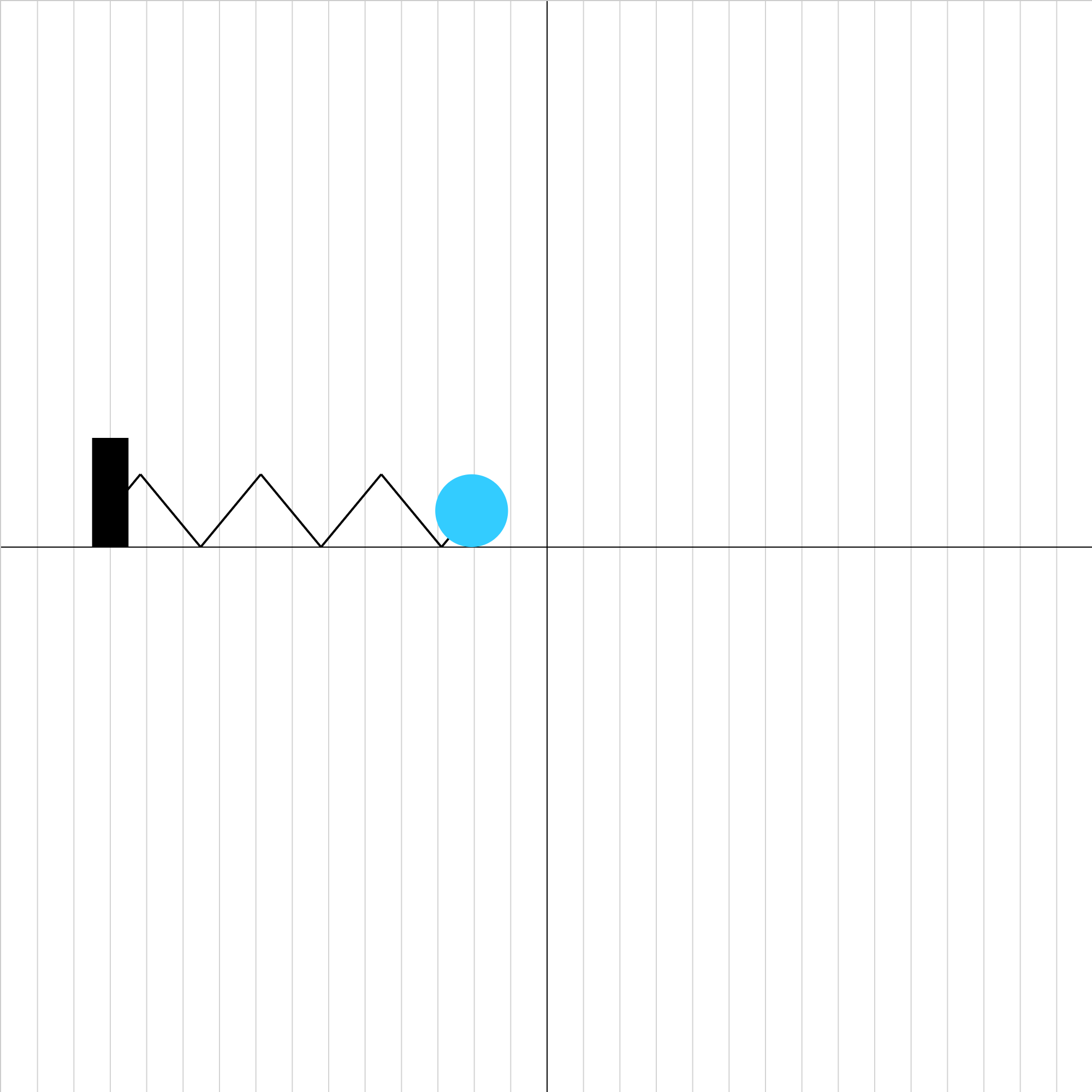
spring-equation-02.iwp
A ball oscillates horizontally in simple harmonic motion on a frictionless surface. Write the equation of the ball's motion. The grid spacing is 0.01 m. Click Show Graph to see graphs of position and velocity vs. time.

spring-equation-03.iwp
A ball oscillates horizontally in simple harmonic motion on a frictionless surface. The ball is initially moving. Write the equation of the ball's motion. The grid spacing is 0.01 m. Click Show Graph to see graphs of position and velocity vs. time.
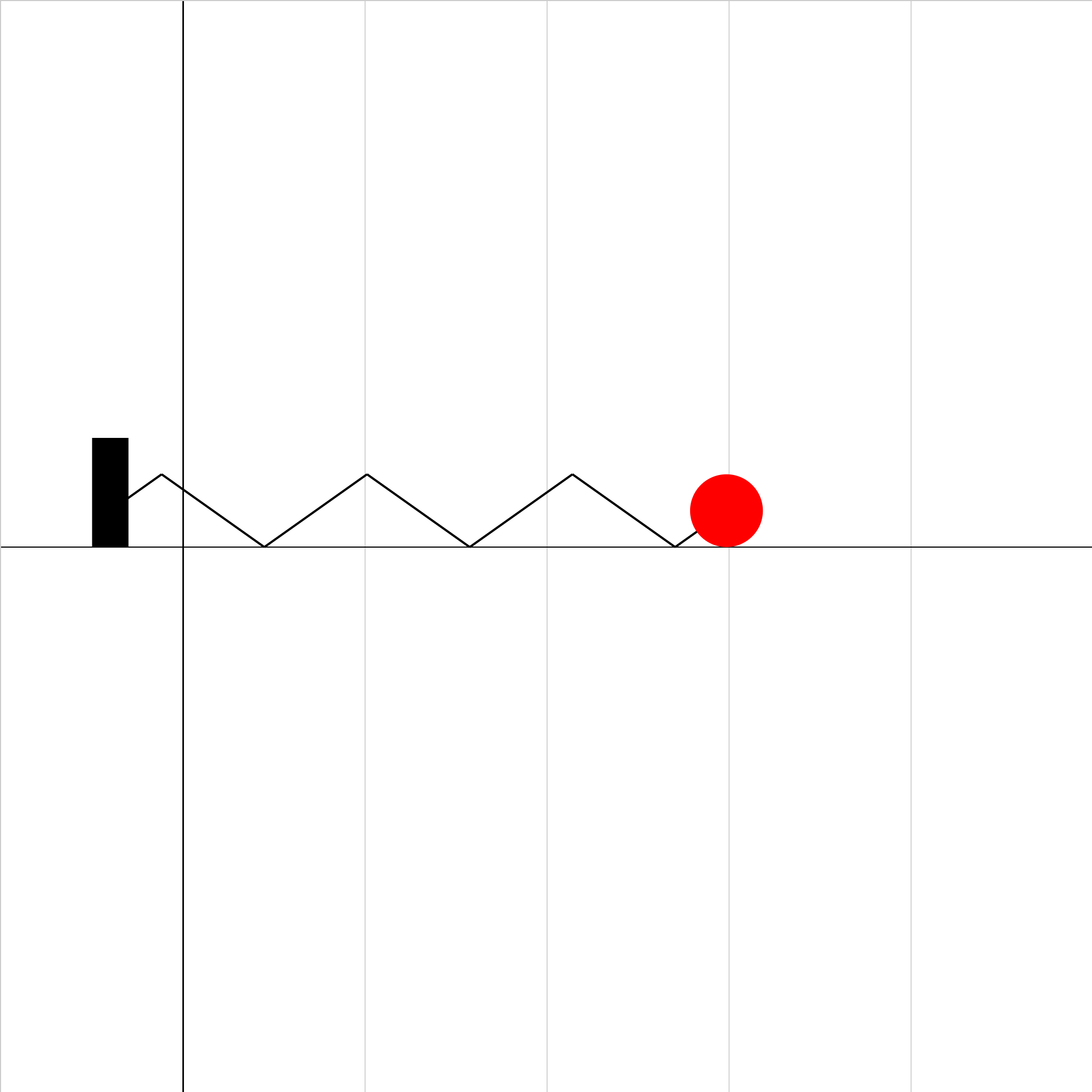
spring-equation-04.iwp
A ball oscillates horizontally in simple harmonic motion on a frictionless surface. Click Show Graph to see graphs of position and velocity vs. time.

spring-motion-4.iwp
When you play the animation, the block oscillates horizontally about the origin on a frictionless table. The origin is in the center, the direction of +x is to the right, and the grid spacing is 0.02 m. The oscillation is the result of a Hooke's Law force applied by the spring to the block. The heights of the vertical bars shown below the table are proportional to the values of kinetic and elastic potential energy of the block-spring system.

stopblock01c.iwp
An object moving horizontally is slowed by a force of kinetic friction. Adjust the magnitude of the initial velocity so that the left side of the block stops at the left-hand edge of the screen.
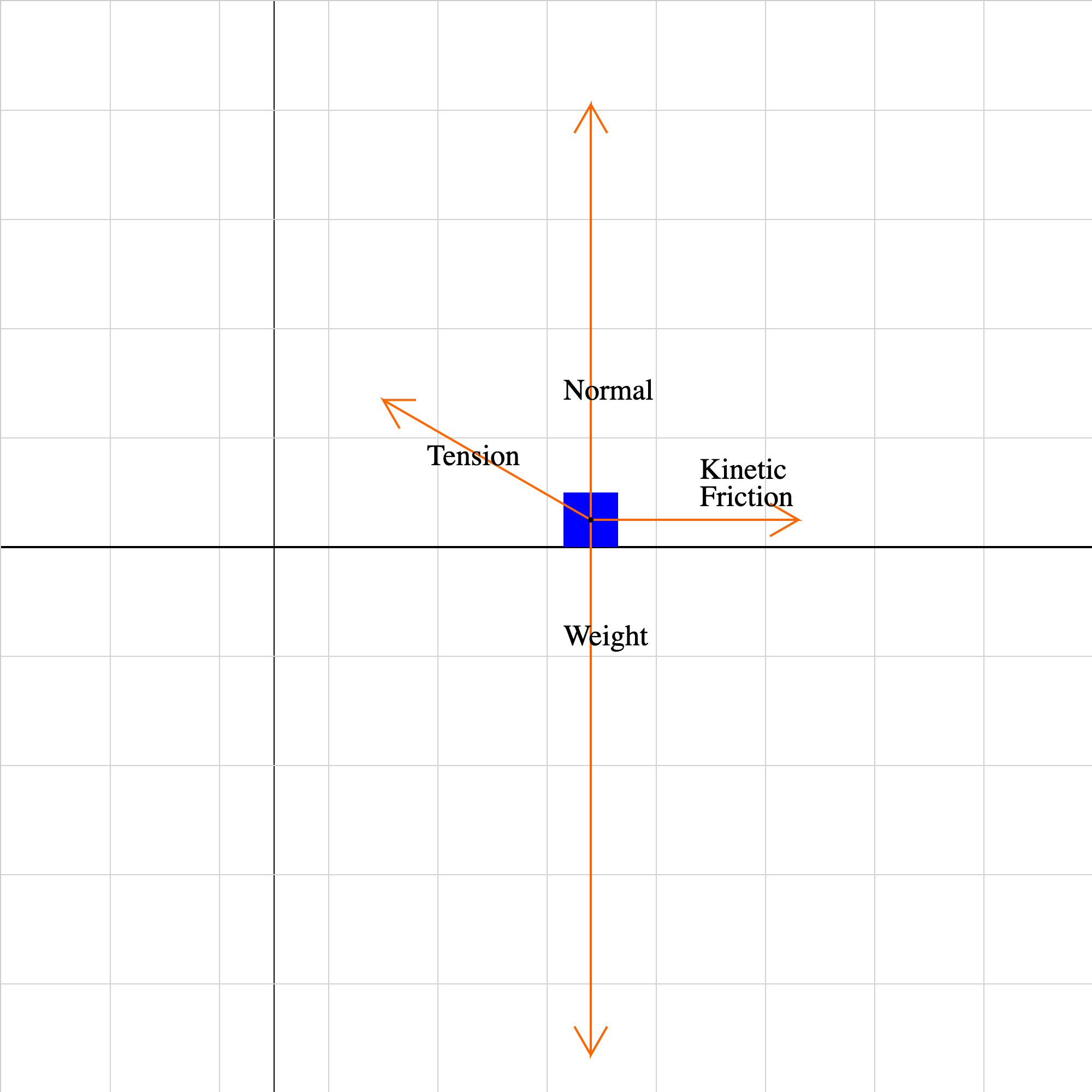
stopblock01f.iwp
An object moves horizontally on a surface at constant velocity under the action of the forces shown.

turntable05.iwp
A penny on a turntable slides off when the turntable reaches a certain frequency. What is the coefficient of static friction of the turntable? How does the result depend on the radius of the path?