Home
Browsing Animations: Oscillations
11 Animations
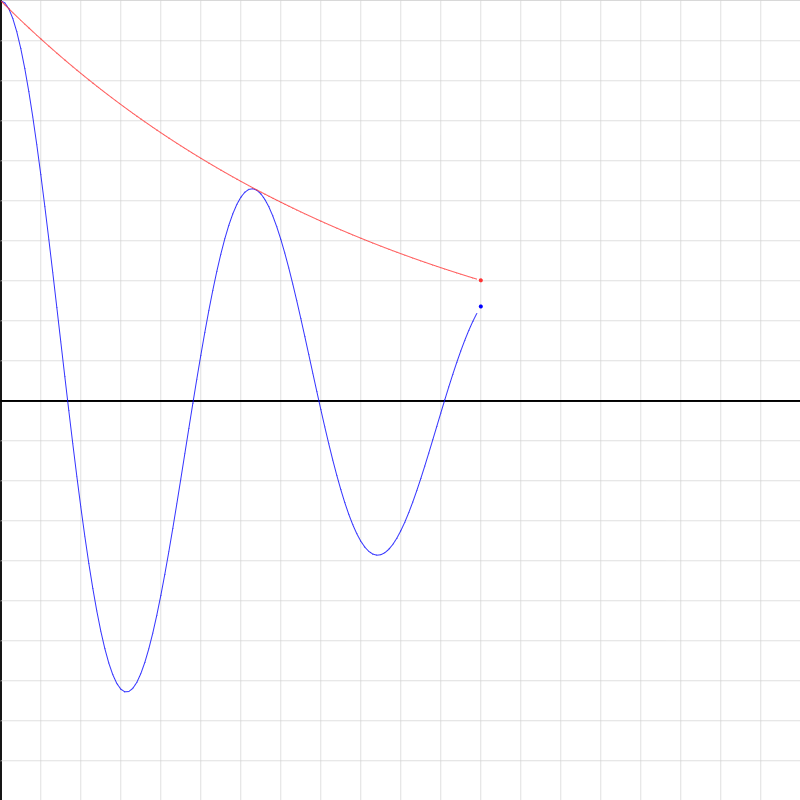
damped-1.iwp
The blue line plots position (vertical) as a function of time (horizontal) for damped SHM. The red line plots the decay of the amplitude.

damped-SHM-template.iwp
This plots position (vertical) as a function of time (horizontal) for an object subject to a Hooke's Law restoring force. Suppose that the object is also subject to a force that always acts opposite the velocity, v, and is proportional to the magnitude of v. If the constant of proportionality is denoted R, then this damping force is -Rv. Investigate the motion for different values of R (say 1, 5, 10, 20).

doppler4.iwp
A source of point spherical waves moves along the x-axis at constant velocity. The current position of the source is indicated by a red dot. Note that the spacing of the dark, vertical grid lines is 200 m. Determine the period of the wave, the velocity of the wave, the velocity of the source, the frequency perceived by an observer at the right edge of the screen, and the frequency perceived by an observer at the left edge of the screen.
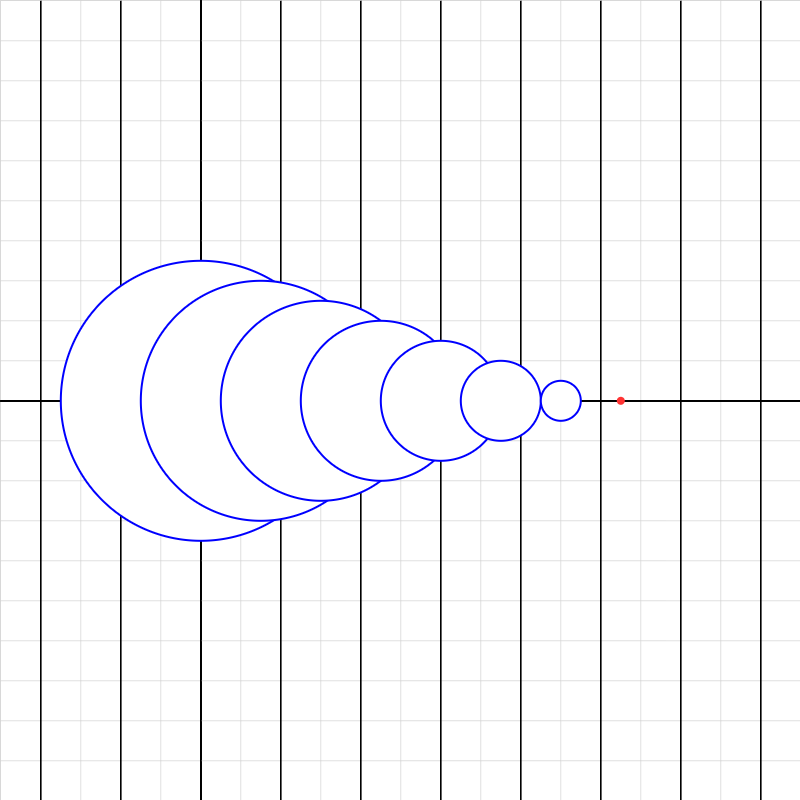
doppler5.iwp
A source of point spherical waves moves along the x-axis at constant velocity. The current position of the source is indicated by a red dot. The spacing of the dark, vertical grid lines is 200 m. Determine the Mach number of the source.

shm-circle-analogy-01.iwp
Demonstration of the circular motion analogy for simple harmonic motion
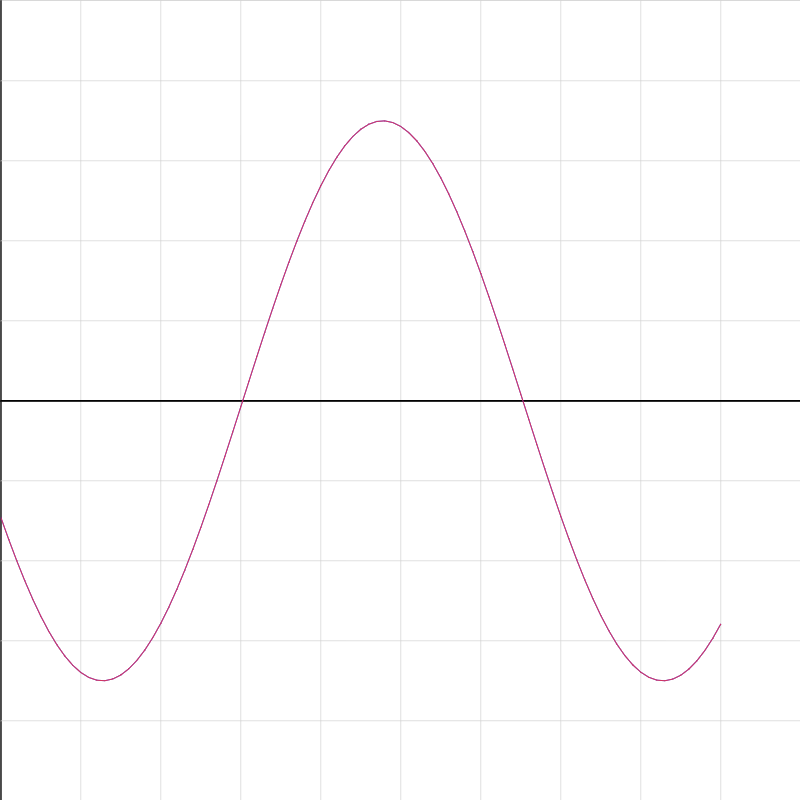
shm-graph-01.iwp
Run the applet to display a position vs. time graph of an object in simple harmonic motion. By entering a value of phase other than 0, a second graph will appear shifted in phase by the amount of the adjustment.
trav-wave-3.iwp
Consider the following model of a linear medium such as a string: a chain of point masses joined by light, strong threads. Traveling waves of constant frequency and wavelength are generated on the medium. The motion of the wave is to the right while the motions of the point masses are vertical. Two particles are marked different colors than the rest. You can display y vs. t graphs of their motion by clicking Show graph.

vertical-spring-01.iwp
A platform (black) of mass 0.0500 kg is suspended from a fixed support by a rubber band that obeys Hooke's Law. Standard masses can be added to the platform in increments of 0.0500 kg. When the red stick is pulled away, the platform with its weight will oscillate vertically about its equilibrium position.
wavedraw.iwp
This applet draws standing wave forms. Diagrams may be screen-captured and imported into documents.