Home
Browsing Animations: Electrostatics
8 Animations
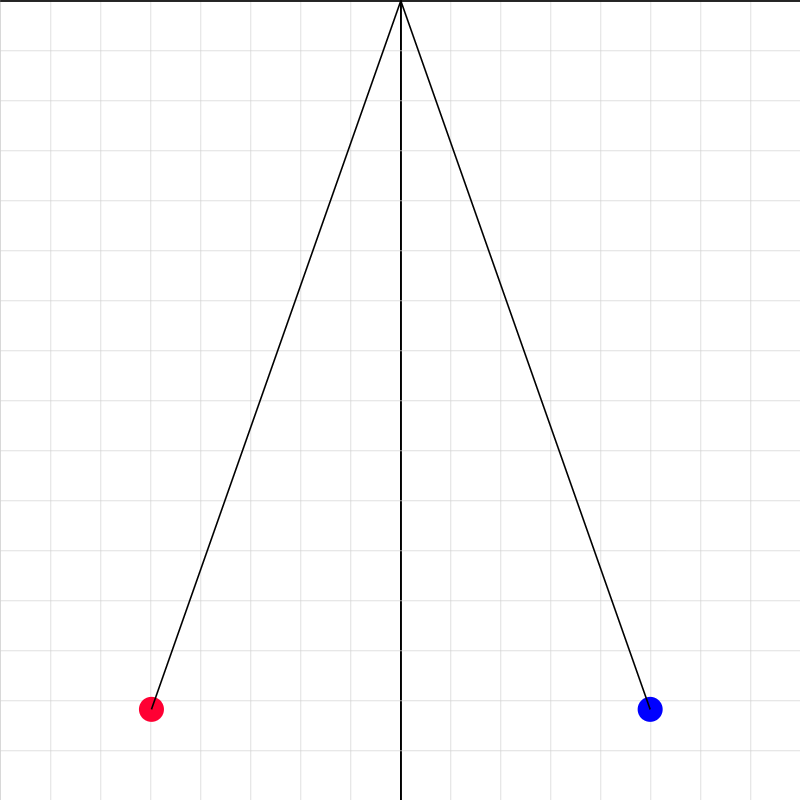
coulombslaw01.iwp
Two balls of equal mass (see Input for value) are suspended from long strings of equal length. The balls are initially charged to the same value of charge Qo. You can add charge to each ball in increments of the initial charge by clicking on the step button (>>). The number by which the charge on each ball is multiplied is listed as an output. The X- and Y-coordinates of the blue ball are also given as outputs. Determine the value of the initial charge Qo. This requires a net force analysis as well as Coulomb's Law. Once you've determined Qo, check your value by changing the mass to something different. Calculate what the separation of the balls should be for that mass. Then check to see if you're right.
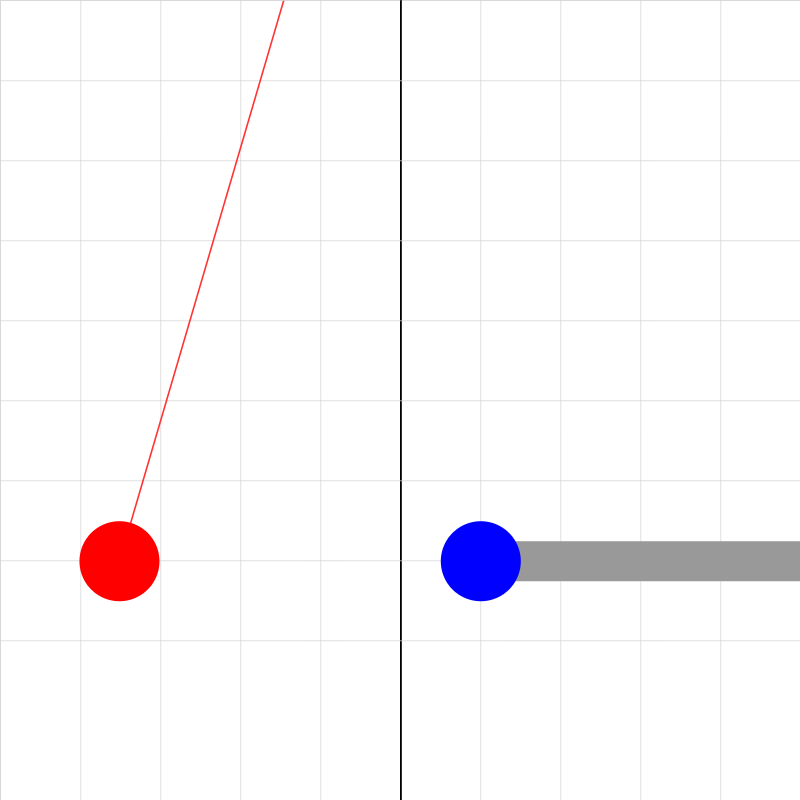
coulombslaw02.iwp
The blue and red balls have the same size, shape, and composition. They have a coating of graphite paint, which makes their surfaces good conductors. The red ball, hanging from a long thread, is initially uncharged while the blue ball has been charged by momentarily touching it to a plastic strip rubbed with fur. The blue ball, which is attached to a horizontal insulating handle, is momentarily touched to the red ball. In order to see the state of the red and blue balls after this momentary contact, click the step button (>>) once. The red ball deflects away from its initial equilibrium position. Note that the X-coordinates of the balls are given as outputs. These enable one to determine the separation of the balls and the horizontal deflection of the red ball. Both of these are related to electrostatic force that either ball exerts on the other. Click on the step (>>) button to move the right charge toward the left in increments of 0.01 m and view the corresponding position of the red ball. (Don't use the play button, >, as this may give incorrect results.) Step through the animation and take data on horizontal deflection of the left ball vs. separation of both balls. Graph and fit the data appropriately. Use a coefficient from the fit to determine the charge on either ball. In order to determine the relationship between the coefficient and the charge, you'll need to do a theoretical force analysis of the situation. In order to simplify the math, assume that the angle that the string makes with the vertical is small. This will allow you to say that the angle and its sine (or tangent) are approximately equal.
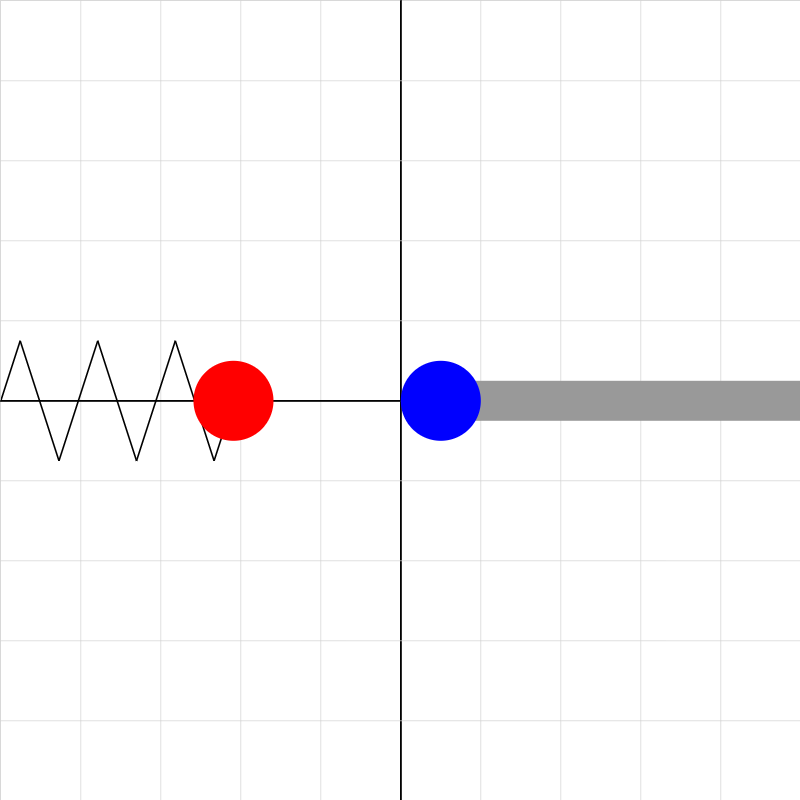
coulombslaw03.iwp
A red ball with charge 5.0E-8 is connected to a spring which is fixed at the left side of the screen. The ball is initially at the unstretched/uncompressed position of the spring, x = 0. A blue ball soon to appear on the right-hand side has the same charge as the red ball. Click the right step button (>>) once. You'll see the blue ball attached to a horizontal insulating handle. The red ball is forced away from its initial position and compresses the spring due to electrostatic force of the blue ball. Click the step button once to move the blue ball to the left. The spring compresses more. The X-coordinates of the balls are given as outputs. These enable one to determine the separation of the balls as well as the displacement of the red ball from equillibrium. Both of these are related to the electrostatic force that either ball exerts on the other. Click on the step (>>) button to move the blue ball toward the left in increments of 0.01 m and view the corresponding position of the red ball. (Don't use the play button, >, as this may give incorrect results.) Something to think about: How does the separation of the balls change as the blue ball moves to the left? Why does this make sense (based on the forces acting on the red ball)?
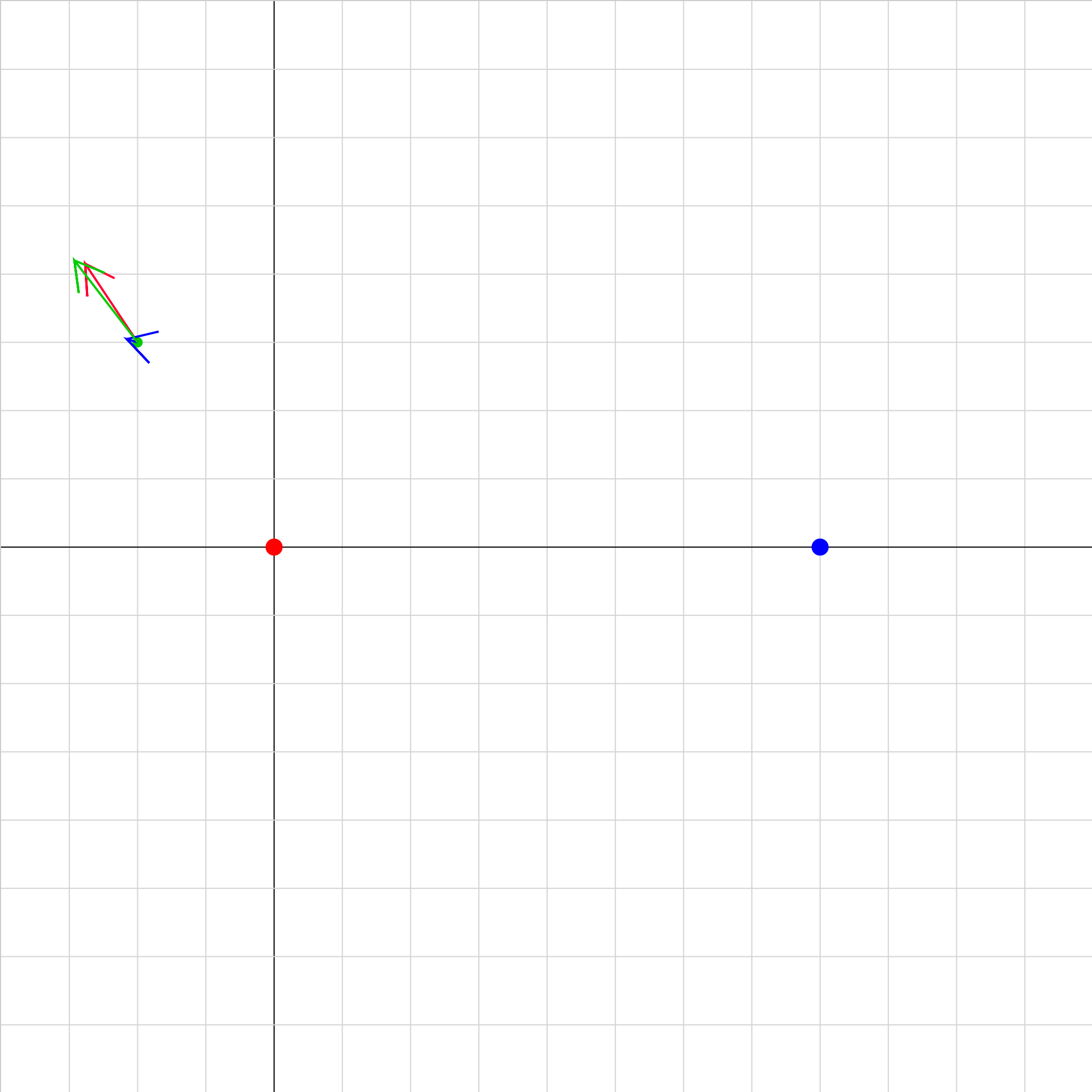
efield-plot-02b.iwp
Two charges (red and blue) are positioned on the x-axis and produce an electric field in the space surrounding them. A positive test charge is represented by the green dot. Vectors representing the magnitude and direction of the fields of the red and blue charges and of the net field are shown at the position of the test charge. Running or stepping the animation will move the test charge across the screen, and the E-field vectors will change accordingly. The direction of motion can be made horizontal or vertical in either direction by the appropriate choice of the X and Y motions: 1 = move horizontally (vertically) to the right (up) 0 = don't move -1= move horizontally (vertically) to the left (down) In addition, the initial coordinates of the test charge can be selected. For easier viewing, the vectors may be scaled to larger or smaller lengths by increasing or decreasing the vector scale factor.
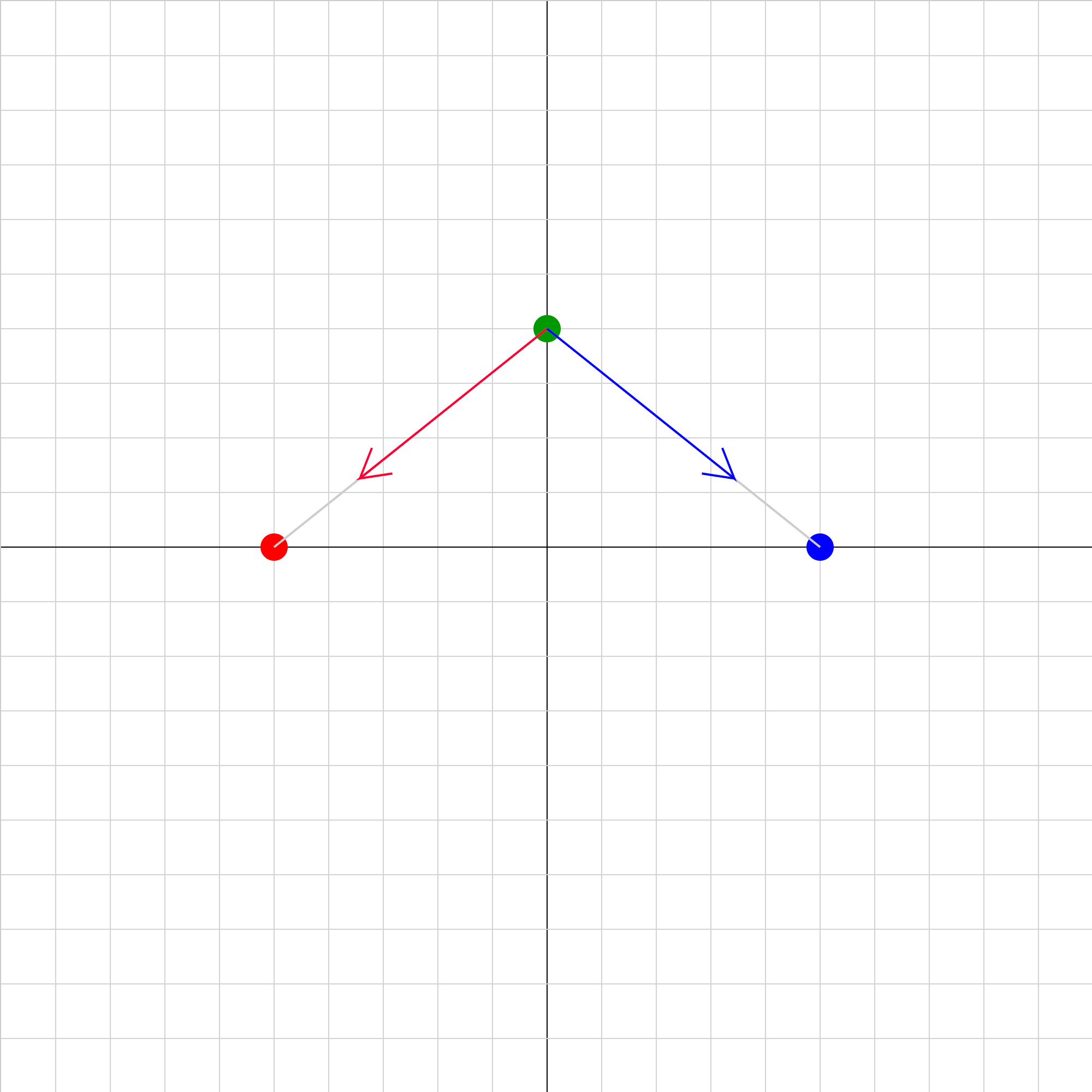
eforce-05.iwp
This is a multiple-choice problem. Enter each of the numbers 1 to 4 in the Choice box. Reset after entering a number. Each choice shows a different version of the electric forces on the positive green charge due to the red and blue charges. Which one of the choices is correct?
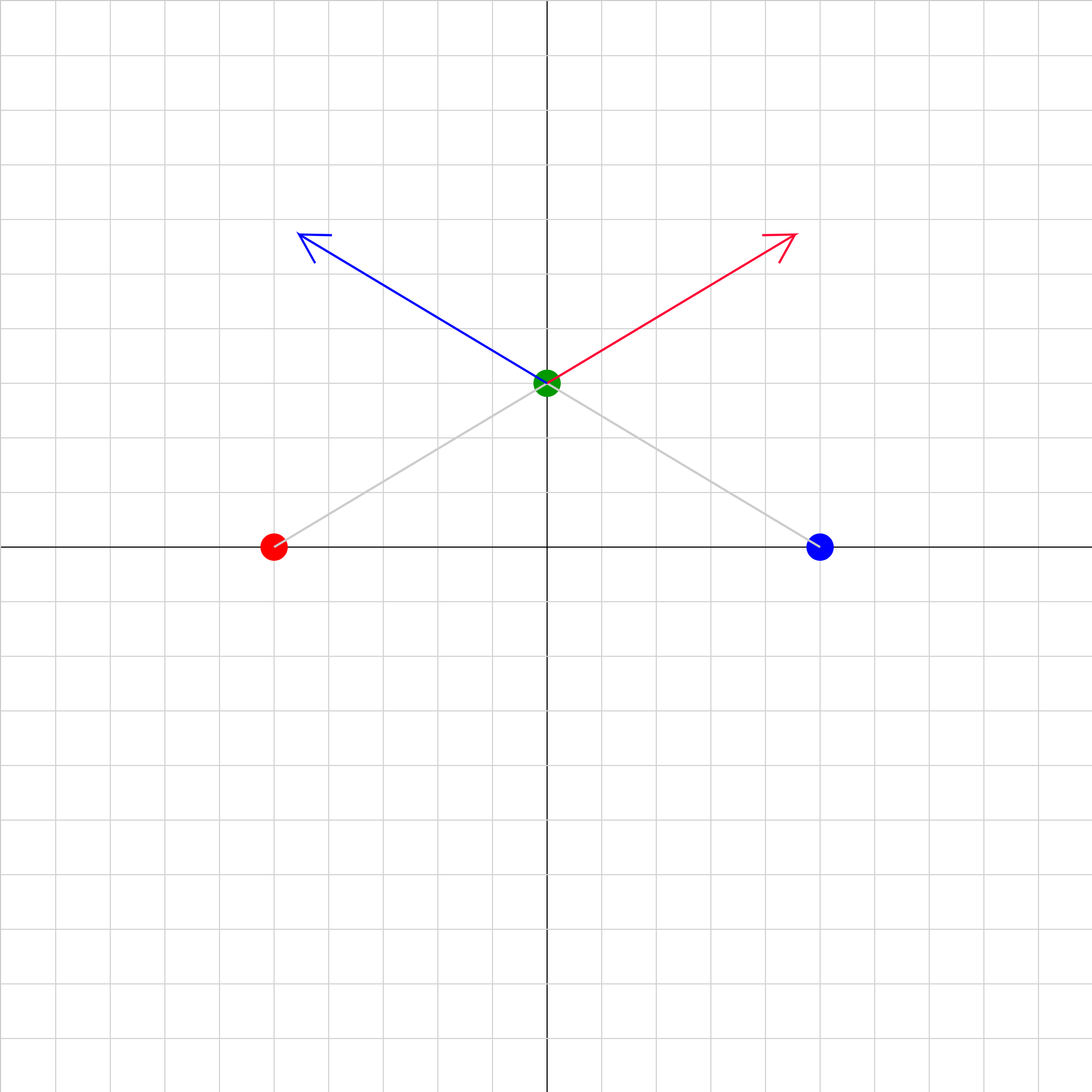
eforce-06.iwp
If the green charge is +1.0 uc (microcoulomb), what are the magnitude and direction of the net electric force on the green charge? Note that all the charges are positive.
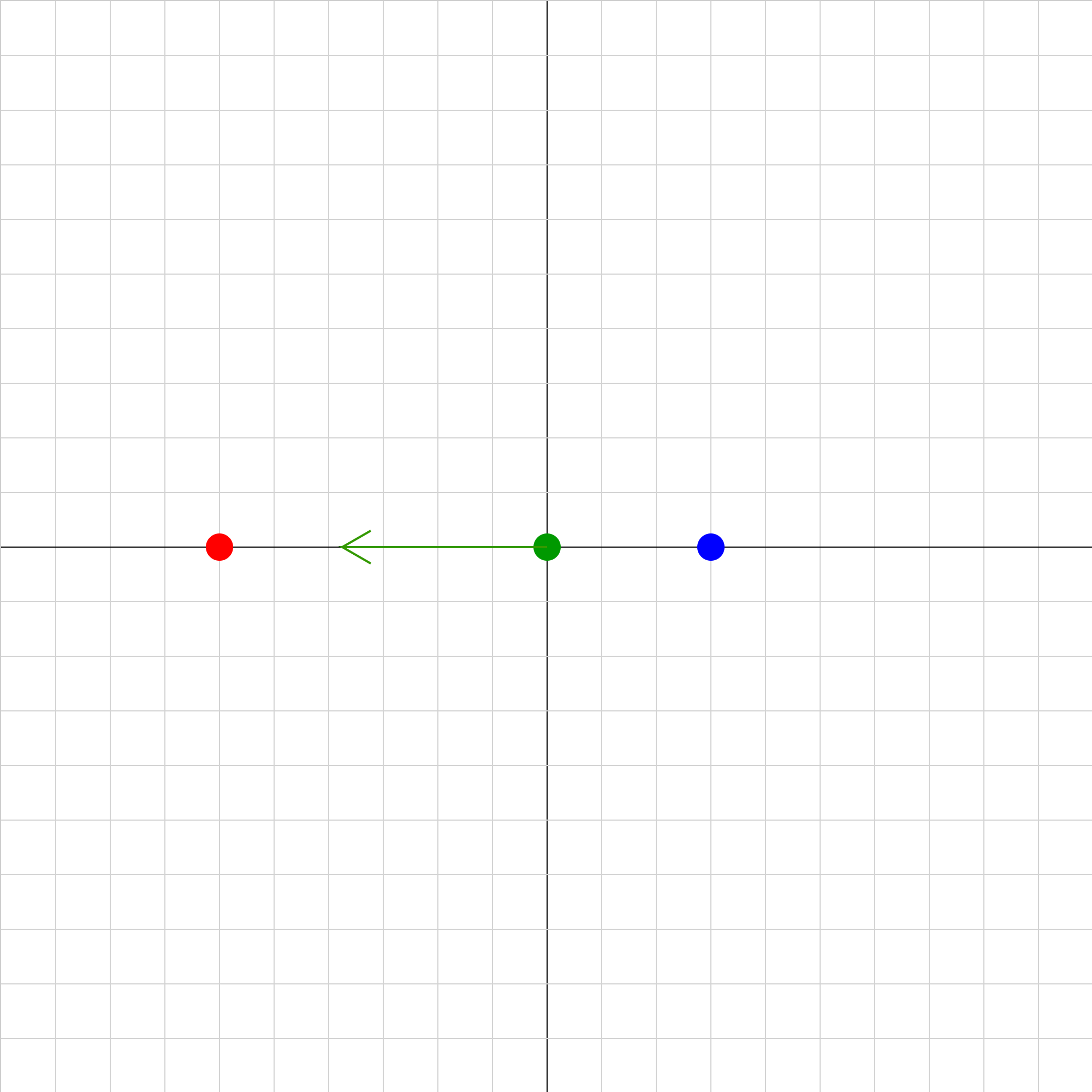
eforce-07.iwp
Two charges (red and blue) are fixed in position on the x-axis. The green vector represents the net electric force on the positive green charge due to the red and blue charges. At what position will the net force on the green charge be 0?
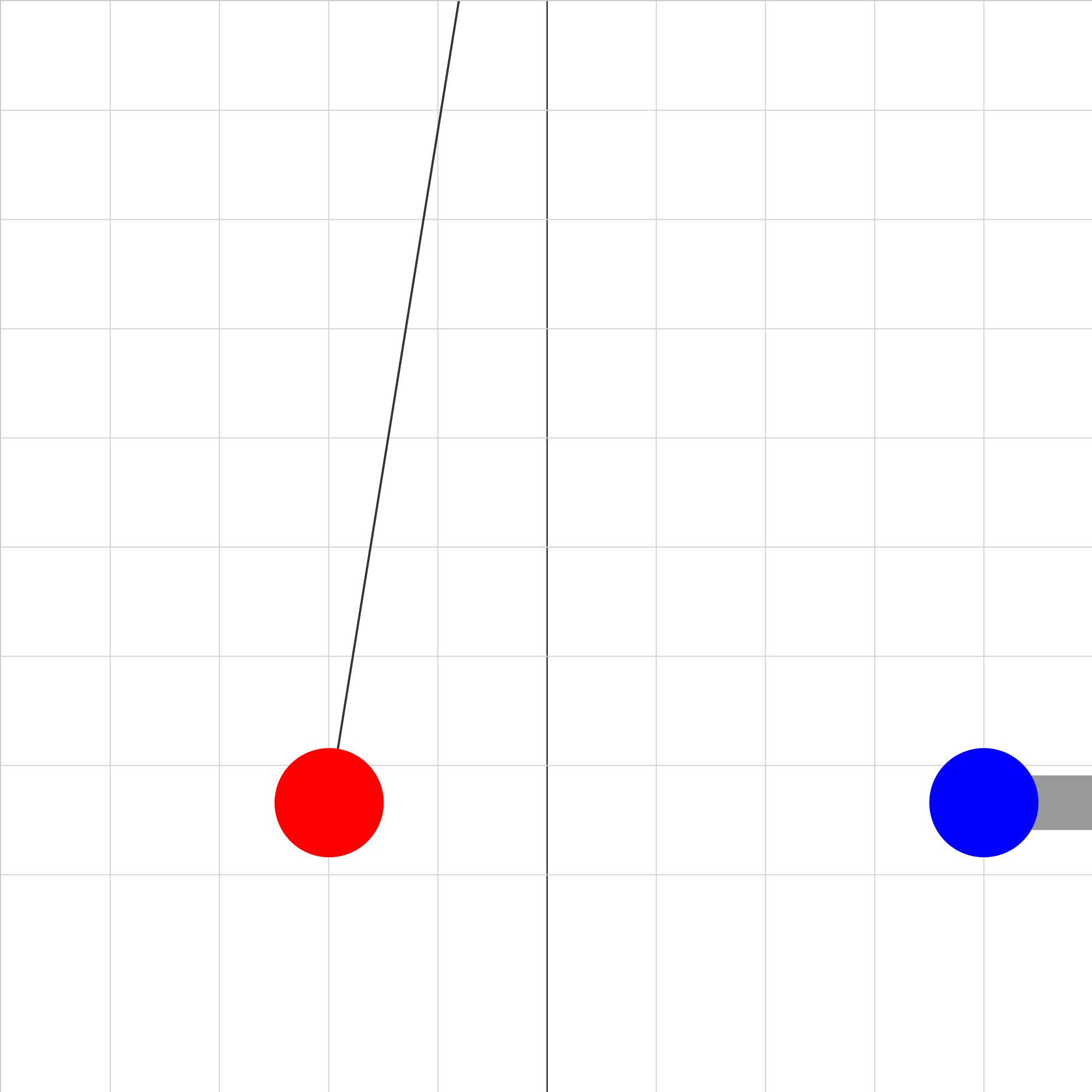
inverse-r-squared-test.iwp
A charged ball hanging from a long thread is deflected to the left by a second charged ball connected to an insulating handle. As the second charge is moved to the left, the first charge deflects more. Determine the relationship between the electric force on the first charge and its separation from the second charge. Click on the step (>>) button to move the right charge toward the left in increments of 0.01 m.